Lowell 1 Peirce MS 455-6 (SPIN) Arisbe Peirce pages on this site

Lecture 2: Existential Graphs, Alpha and Beta

Charles S. Peirce: second of the Lowell Lectures of 1903, previously published in NEM 3, pp. 405-430.
Robin catalogue: MS. 455, notebook, 1903, pp. 1-31: The first and third parts of an introduction to the alpha and beta parts of the system of existential graphs; MS. 456 is the second part: 1903, pp. 40-66.
[note: This version of Lowell Lecture 2 is based on my transcription of the manuscripts, done in September-October 2017 using the tools provided online by the SPIN project. Any transcription errors are mine alone. I have occasionally altered punctuation for clarity. —Gary Fuhrman, 3 December 2017

Let us take up the subject of necessary reasoning, mathematical reasoning, with a view to making out what its elementary steps are and how they are put together.

In order to do this it is necessary to replace the confused syntax of ordinary language by a system in which the meaning of every form is exactly defined, which is free from forms that cast a tinge of passion or of any kind of subjective feeling on the facts, and which has no more forms than are requisite in order to express every kind of fact or truth in such a way as to enable us to carry the dissection of reasoning to its smallest steps.

Let us devote this evening's hour to forming such a system of expression.

Before beginning, let us distinctly recognize the purpose which this system of expression is designed to fulfil. It is intended to enable us to separate reasoning into its smallest steps so that each one may be examined by itself. Observe, then, that it is not the purpose of this system of expression to facilitate reasoning and to enable one to reach his conclusions in the speediest manner. Were that our object, we should seek a system of expression which should reduce many steps to one; while our object is to subdivide one step into as many as possible. Our system is intended to facilitate the study of reasoning but not to facilitate reasoning itself. Its character is quite contrary to that purpose.

Let the blackboard represent the universe. As thus significant we will call it the sheet of assertion.

Let whatever I write upon the blackboard or sheet of assertion go toward making the representation of the universe more determinate. Thus, I write

That represents that there is a pear and a ripe pear in the universe.

Necessary reasoning can never answer questions of fact. It has to assume its premisses to be true. Therefore, in order to avoid the possibility of questioning what is written on the board, let us say that it is not the real universe that is represented by the board, but a universe existing in my imagination, concerning which you have no source [of] information except my testimony. By the universe I mean the entire collection of things, or subjects of force, to which all that is going to be written on the board will relate. Logicians call such a collection of things, or subjects of force, to which the whole of a discussion relates, the universe of discourse.

This universe consists in the first place of certain mutually well-understood centres, or subjects of force well-understood to be different from one another; secondly, of certain subjects of force well-understood to exist, but not thoroughly understood to be known to be different from any of these of the first class; and thirdly of an indefinite supplement of subjects of force presumed to exist but of which there has been no definite recognition. Summing up the matter, we may say that the universe of discourse is the aggregate of subjects of the complexus of experience-forces well-understood between the graphist, or he who scribes the graph, and the interpreter of it.

The system of expression which I have thus begun to describe will be found to be a system of diagrams. The mathematicians call a diagram that is composed mainly of spots of different kinds and lines, a graph. This system is called a system of existential graphs. In this system, the spots may be conveniently differentiated from one another by words written in them. The consequence is that a sign of this system is party drawn and partly written. For brevity, I always say it is scribed. Any sign conforming to the rules of this system which, if it were placed on the board or sheet of assertion, would assert some intelligible state of things to be true of the universe of discourse, is called a graph. Strictly, I ought to say an existential graph; but for brevity since existential graphs will be the only ones dealt with, I shall call it a graph, simply. For example, what I have just scribed is a graph. The board itself is a graph, since it represents the universe as consisting of single imaginary things. The board and what is written on it together make up another graph.

It is quite important, however, to distinguish between a graph and a graph replica. Suppose an editor writes to me and asks for an article of 4000 words. You know what he means by words in that case. In what I write the single word “the” may occur twenty times on every page. Every time it will count as a separate word. Yet in another sense, it is the same word. In this latter sense, the word the consists in the sum total of general conditions to which ink-marks or voice-sounds must conform in order to be understood in a certain way.

In this sense the word the is, strictly speaking, never written; but what is written conforms to it, or, as we say, embodies it. In the other sense a written word is written once and only once, since every act of writing makes a new word. Now when I speak of a graph, I mean the general type of whatever means the same thing and expresses that meaning in the same way so far as the conventions of this system take cognizance of the ways; while that which is scribed once and only once and embodies the graph, I call a graph-replica. For brevity, however, I speak of “scribing a graph” just as we speak of writing the word the. The phrase may be defended as employing the word “scribe” in a special sense. I will now put an additional replica upon the board, or the sheet of assertion

Let us agree to understand that each of those replicas has the same meaning as if it stood alone; and that it shall be the same with any other two replicas on the sheet, so that I now assert not only that there is a ripe pear, but also that it rains.

By calling this system a system of existential graphs, my meaning is that two graphs at different points of the board, whether far or near, are both asserted, each just as much as if the other were not there.

The most immediately useful information is that which is conveyed in conditional propositions, “If you find that this is true, then you may know that that is true.” Now in ordinary language the conditional form is employed to express a variety of relations between one possibility and another. Very frequently when we say “If A is true, then B is true,” we have in mind a whole range of possibilities, and we assert that among all possible cases, every one of those in which A is true will turn out to be a case in which B is true also. But in order to obtain a way of expressing that sort of conditional proposition, we must begin by getting a way of expressing a simpler kind, which does not often occur in ordinary speech but which has great importance in logic. The sort of conditional proposition I mean is one in which no range of possibilities is contemplated, which speaks only of the actual state of things. “If A is true then B is true,” in this sense is called a conditional proposition de inesse. In case A is not true, it makes no assertion at all and therefore involves no falsity. And since every proposition is either true or false, if the antecedent, A, is not true, the conditional de inesse is true, no matter how it may be with B. In case the consequent, B, is true, all that the conditional de inesse asserts is true, and therefore it is true, no matter how it may be with A. If however the antecedent, A, is true, while the consequent, B, is false, then, and then only is the conditional proposition de inesse false. This sort of conditional says nothing at all about any real connection between antecedent and consequent; but limits itself to saying “If you should find that A is true, then you may know that B is true,” never mind the why or wherefore.

For a more detailed explanation of this point of logic, see this excerpt from the second of Peirce's 1898 Cambridge lectures (R441, RLT 125-6, NEM4 169-70):

Cicero informs us that in his time there was a famous controversy between two logicians, Philo and Diodorus, as to the signification of conditional propositions. Philo held that the proposition “if it is lightening it will thunder” was true if it is not lightening or if it will thunder and was only false if it is lightening but will not thunder. Diodorus objected to this. Either the ancient reporters or he himself failed to make out precisely what was in his mind, and though there have been many virtual Diodorans since, none of them have been able to state their position clearly without making it too foolish. Most of the strong logicians have been Philonians, and most of the weak ones have been Diodorans. For my part, I am a Philonian; but I do not think that justice has ever been done to the Diodoran side of the question. The Diodoran vaguely feels that there is something wrong about the statement that the proposition “If it is lightening it will thunder” can be made true merely by its not lightening.

Duns Scotus, who was a Philonian , as a matter of course, threw considerable light upon the matter by distinguishing between an ordinary consequentia, or conditional proposition, and a consequentia simplex de inesse. A consequentia simplex de inesse relates to no range of possibilities at all, but merely to what happens, or is true, hic et nunc. But the ordinary conditional proposition asserts not merely that here and now either the antecedent is false or the consequent is true, but that in each possible state of things throughout a certain well-understood range of possibility either the antecedent is false or the consequent true. So understood the proposition “If it lightens it will thunder” means that on each occasion which could arise consistently with the regular course of nature, either it would not lighten or thunder would shortly follow.

Now this much may be conceded to the Diodoran, in order that we may fit him out with a better defence than he has ever been able to construct for himself, namely, that in our ordinary use of language we always understand the range of possibility in such a sense that in some possible case the antecedent shall be true. Consider, for example, the following conditional proposition: If I were to take up that lampstand by its shaft and go brandishing the lamp about in the faces of my auditors it would not occasion the slightest surprise to anybody. Everybody will say that is false; and were I to reply that it was true because under no possible circumstances should I behave in that outrageous manner, you would feel that I was violating the usages of speech.

I would respectfully and kindly suggest to the Diodoran that this way of defending his position is better than his ordinary stammerings. Still, should he accept my suggestion I shall with pain be obliged to add that the argument is the merest ignoratio elenchi which ought not to deceive a tyro in logic. For it is quite beside the question what ordinary language means. The very idea of formal logic is, that certain canonical forms of expression shall be provided, the meanings of which forms are governed by inflexible rules; and if the forms of speech are borrowed to be used as canonical forms of logic it is merely for the mnemonic aid they afford, and they are always to be understood in logic in strict technical senses. These forms of expression are to be defined, just as zoologists and botanists define the terms which they invent, that is to say, without the slightest regard for usage but so as to correspond to natural classifications. That is why I entitled one of the first papers I published, “On the Natural Classification of Arguments.” And by a natural classification, we mean the most pregnant classification, pregnant that is to say with implications concerning what is important from a strictly logical point of view.

Now I have worked out in MS. the whole of syllogistic in a perfectly thoroughgoing manner both from the Philonian and from the Diodoran point of view. But although my exposition is far more favorable to the Diodoran system even than that of DeMorgan in his Syllabus of Logic, which is much the best presentation of the Diodoran case ever made by an adherent of it, yet I find that the Philonian system is far the simpler,— almost incomparably so. You would not wish me to take you through all those details. This general statement is all that is appropriate for this brief course of lectures.

Be it understood, then, that in logic we are to understand the form “If A, then B” to mean “Either A is impossible or in every possible case in which it is true, B is true likewise,” or in other words it means “In each possible case, either A is false or B is true.”

The question of the proper way of expressing a conditional proposition de inesse in a system of existential graphs has formed the subject of an elaborate investigation with the reasoning of which I will not trouble you. Suffice it to say that it is found that there is essentially but one proper mode of representing it. Namely, in order to assert of the universe of discourse that if it rains then a pear is ripe I must put on the blackboard this:

I draw the two ovals which I call a scroll in blue because I do not want you to regard them as ordinary lines. I want you to join me in making believe that they are cuts through the surface, and that inside the outer one the skin of the board has been stripped off disclosing another surface below. This I call the bottom or area. Therefore “It rains” is not scribed on the blackboard or, as I say, is not scribed on the sheet of assertion. For what is scribed on that sheet is asserted to be true of the universe of discourse; while the statement “It rains” is a mere supposition. Let us say that that bottom inside the outer cut represents another universe, a universe of supposition, and that it is only in that universe that it is said to rain. Besides this graph, “It rains” the bottom of the outer cut contains the inner cut which interrupts its surface; and inside the inner we will make believe that a patch is put in with a surface like that of the blackboard, although cut off from it. I use the word area for any part of the surface [unbounded?] or bounded by cuts, never extending [through?] a cut.

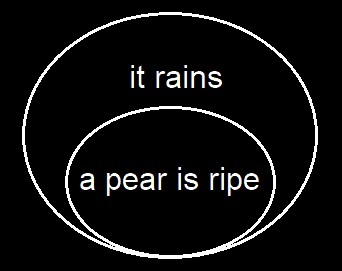
A fixed terminology is a great comfort. Let us term the area on which a cut stands the place of the cut, while the area or bottom of the cut is the area within the cut. The cut itself is not a graph nor the replica of a graph. No more is the scroll. But the scroll with the two graphs scribed in its two closes or areas makes up a graph, or graph-replica; and this I call an enclosure. The term may be used indifferently to mean the graph or the replica.

In order to get an insight into how the scroll represents the conditional proposition de inesse, we must make a little experimental research.

Thus far, we have no means of expressing an absurdity. Let us invent a sign which shall assert that everything is true. Nothing could be more illogical than that statement, inasmuch as it would render logic false as well as needless. Were every graph asserted to be true, there would be nothing that could be added to that assertion. Accordingly, our expression for it may very appropriately consist in completely filling up the area on which it is asserted. Such filling up of an area, may be termed a blot.

Take the conditional proposition de inesse, “If it rains then everything is true[”:]

That amounts to denying that it rains. But there is no need of making the inner cut so large. Let us write
or even
This suggests that the relation which the cut asserts between the universe of discourse and what is scribed within it is simply that what is scribed within is false of the universe of discourse.

Then we may interpret

as meaning “It is false that it rains and that a pear is not ripe.” But we have already seen that this is precisely the whole meaning of the conditional de inesse; namely that it is false that the antecedent is true while the consequent is false. Thus, that which the cut asserts is precisely that that which is on its bottom is not, as a whole, true.

This agrees with the fact that if there is nothing on the bottom except the inner cut, its patch may be asserted. Thus

since a blank merely asserts known truth means, “if the truth is true then a pear is ripe,” or it is not false that a pear is ripe. So in the following
or if it rains, then if it blows, a pear is ripe. The two cuts with nothing between can be taken away without altering the fact expressed
If it both rains and blows a pear is ripe.

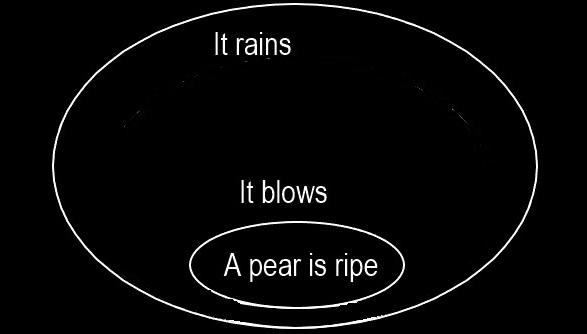
So much of the system of existential graphs as I have thus far described I term the alpha part of the system. I shall presently describe a beta part, and in another lecture the system will be completed by a gamma part.

There are certain ways in which graphs that are scribed on the sheet of assertion can be modified without any danger of changing a true graph into a false one. Transformations according to any general method that can never change a true graph into a false one I term permissible transformations. In particular, those which the principles of the alpha part of the system render permissible shall be termed alpha permissible transformations, and in general I shall use “alpha” freely as a prefix to signify a reference to these principles. Thus, I shall say that the alpha-signs, that is to say the signs of this system heretofore described apart from the graphs themselves, are two, and there are besides two peculiar graphs. Namely, the two peculiar graphs are the blank place which asserts only what is already well-understood between us to be true, and the blot which asserts something well understood to be false. The two signs which are not graphs are the putting of two graph-replicas upon the same area, which if we remember that a blank is a graph, is seen to include the scribing of a single graph as a special case. This idea that scribing a graph is a transformation of a graph already accepted is a very useful one. The other sign is the scroll.

I have just defined a permissible transformation as one which conforms to a general type which in no case can transform a true graph into a false one. But what do we mean by a true graph and a false one? I will not stop at present to analyze fully the meaning, because this system of existential graphs is not intended to inquire into the conformity of thoughts to experiences. The universe of our discourse is to be a universe of my imagination, and therefore any graph which I permit to be scribed will be true, unless it is absurd and so amounts to telling you that my universe has no being even in my imagination. Therefore, for our purposes, a true graph is nothing but a graph which will result from a special permission to transform the blank sheet of assertion into the sheet with that graph scribed upon it. As for the general alpha-permissions, they are nothing but the definitions of the four general Alpha signs in terms of permissibility.

Let us draw up statements of them. You know that every definition consists of two propositions. Thus if man is defined as a featherless biped, the one proposition Every man is a featherless biped predicates the definition ‘featherless biped’ of the definitum, ‘man’; while the other proposition ‘Every featherless biped is a man’ predicates the definitum of the definition.

Consequently, each sign of the system should furnish us with two permissions of transformation.

Beginning then with the sign which consists in scribing together, or as we may term it, compounding, the definition of it in terms of permission will be

1st, predicating the definition of the definitum, if it is permitted to scribe on the sheet of assertion a replica of a compound graph, then it is permitted to scribe on the sheet of assertion a replica of either component. Or, stating this in terms of transformations: Any replica of a compound graph may on the sheet of assertion be transformed into a replica of either component. That is to say, under a more practical aspect, any partial graph on the sheet of assertion may be erased or cancelled. This shall head our list of alpha permissions[:]

Permission No 1. Any graph on the sheet of assertion can be erased.

2nd, predicating the definitum of the definition: if it be permitted to scribe on the sheet of assertion a replica of which we please of two graphs then it is permitted to scribe the replica of the compound graph of which those two are the sole components. Or in terms of transformation, if it be permitted to transform the blank sheet into either we please of two graphs, it is permissible to transform it into the compound of the two. That is to say, under a more practical aspect, whatever might be scribed on the sheet of assertion were this blank, can be scribed regardless of what is already scribed. This shall be our second alpha permission.

Permission No 2. Whatever is permissively scribable on the sheet of assertion is so regardless of what is already scribed.

Let us now treat the scroll in the same way.

First, the predication of the definition with the definitum as subject is that when it is permitted to scribe upon the sheet of assertion a scroll with two graph-replicas, x and y, in its outer and in its inner close, or on its bottom and on it[s] patch, respectively,

then whenever it is permitted to put the graph x upon the sheet of assertion, it will likewise be permitted to put the graph y upon the sheet of assertion. Or in terms of transformation it will be permissible on the sheet of assertion to transform x by the insertion into it of y as a component of a compound graph xy.

In order to put this into a more explicit shape, I will first call your attention to a corollary from it. A corollary to a proposition of Euclid is a necessary consequence drawn from it by some editor of Euclid's Elements and inserted by him, originally, I suppose, marked with a little crown in the margin. These additions are, for the most part, propositions that Euclid thought too obvious for special notice. Hence, any easily drawn necessary consequence of a proposition is termed a corollary. Here I will tell you a secret about necessary consequences. It is a very useful thing to know, although most logicians are entirely ignorant of it. It is that not even this simplest necessary consequence can be drawn except by the aid of Observation, namely the observation of some feature of something of the nature of a diagram, whether on paper or in the imagination. I draw a distinction between Corollarial consequences and Theorematic consequences. A corollarial consequence is one the truth of which will become evident simply upon attentive observation of a diagram constructed so as to represent the conditions stated in the conclusion. A theorematic consequence is one which only becomes evident after some experiment has been performed upon the diagram, such as the addition to it of parts not necessarily referred to in the statement of the conclusion. In the present case, I am going to draw a conclusion about a double enclosure that is, two cuts one within the other and with the annular space between them blank like this

The observation which I ask you to make is that in every such case there will be a graph of which one replica is in the outer close while another is on the sheet of assertion outside. Namely, that graph is the blank. And since the present principle permits us to transform
[into]
whatever x may be, it allows this transformation when x is the blank; so that we can transform
into

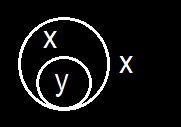
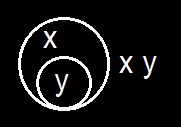
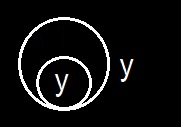
We may count this as our third permission, so that we have

Permission No 3. A graph within a double enclosure on the sheet of assertion may be scribed on the sheet of assertion, unenclosed.

The consideration of what further explicit permission is involved in the predication of the definition, the definitum being the subject, had better be postponed until we have considered the predication of the definitum the definition being the subject. This predication is that in case the permission to scribe on the sheet of assertion a replica of a graph, x, would carry with it in every case a permission to scribe on the sheet of assertion a replica of a graph, y, then it is permissible to scribe on the sheet of assertion a scroll containing in its outer close only a replica of x and in its inner close a replica of y. Or in terms of transformation, if it would be permissible to transform a graph, x, should it occur on the sheet of assertion, into a graph, y, then it is permissible to transform a blank on the sheet of assertion into a scroll having only x in its outer close and having y in its inner close.

We may here draw a corollary analogous to [?], but much more obvious. Namely, To say that it is permissible to scribe any graph, y, on the sheet of assertion is to say that it is permissible to transform a replica of the blank into a replica of y. But this, according to this part of the definition of the scroll, permits us to place on the sheet of assertion the scroll

Hence we have

Permission No 4. If a graph could be permissively scribed on the sheet of assertion a double enclosure containing that graph may be placed on the sheet of assertion.

By combining the two parts of the definition of the scroll we get the highly useful graphical form of the principle of contraposition. Namely, suppose that a replica of the graph x, were it scribed on the sheet of assertion, would be permissively transformable into a replica of the graph, y, and suppose that the scroll

were permissively placed on the sheet of assertion. Then, by the predication of the definition concerning the definitum, y, if scribed on the sheet of assertion, would be transformable into z. So x being transformable into y and y in its turn into z, it follows that x would on the sheet of assertion be transformable into z. Hence by the predication of the definitum concerning the definition, it would be permitted to place on the sheet of assertion the scroll
That is to say, the permissibility of the transformation on the sheet of assertion of x into y, carries with it the permissibility of the transformation on the bottom of a cut placed on the sheet of assertion, of the reverse transformation of y into x. Here is a principle which involves many permissions.

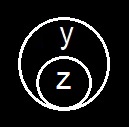
Permission No 5
The Principle of Contraposition.
Of whatever transformation is permissible on the sheet of assertion, the reverse transformation is permissible within a single cut.

Thus if

and so on indefinitely. In short, whatever transformation is permissible on the sheet of assertion is permissible within any even number of cuts while the reverse transformation is permissible within any odd number of cuts. For example, since any graph can be erased on the sheet of assertion any graph can be erased within any even number of cuts while any graph can be inserted within any odd number of cuts. Since any graph already scribed on the sheet of assertion can by Permission No 2 be iterated on the sheet of assertion, that is can have another replica of it placed on the sheet, it follows that if one replica of a graph is on the sheet of assertion and another replica of the same graph is oddly enclosed, the latter can be erased. Thus,
can be transformed into
and thence by Permission No 3 into x y, and thence by Permission No 1 into y. Thus what the logic books call the modus ponens
gives successively
it is cold.
The fact that our system breaks this up into three steps goes to show that our main purpose, that of dissecting reasoning into its simplest elements, has been, in some measure, at least, attained.

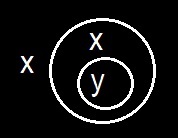
It still remains to treat the blank and the blot in the same manner.

But when we undertake to predicate of the blank as definitum any definition we find that no specific permission follows from the existence of a blank, although the whole possibility of writing graphs depends upon it. That has therefore to be passed over. As to the predication of the definition concerning the definitum, this renders it permissible for a blank to accompany any and every graph scribed on the sheet of assertion. It is truly fortunate that this is permitted, inasmuch as it would be physically impossible that a blank should not accompany every graph. The truth is that the system of existential graphs was intentionally contrived so that this matter should take care of itself. Here, again, therefore, no permission is called for.

Passing to the blot, or pseudograph, of which you remember the meaning is that everything is true, the predication of the definition concerning the definitum is that within any even number of cuts, where the blot is any graph we please may be inserted, and within any odd number of cuts, where the blot is any graph may be erased. The blot, it is true, fills its whole area, so as to leave no room for any other graph. But there is an equivalent of it of which this is not true. For since by Permission No 1 every graph on the sheet of assertion can be transformed into the blank, it follows by the principle of contraposition that an enclosure containing nothing but a blank can when evenly enclosed be transformed into anything we please, and consequently into the pseudograph. The vacant enclosure is, therefore, a form of the pseudograph. For evenly enclosed it can be transformed [into] the blot, or the blot can be transformed into it. And since these two transformations are the reverse of one another, it follows, by the principle of contraposition, that the same is true within any odd number of cuts. When the vacant enclosure is oddly enclosed as in this figure

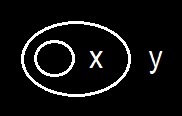
the enclosure on whose area it stands is evenly enclosed and can be erased by Permission No 1. But when the vacant enclosure is evenly enclosed as in the next figure
all other graphs in the same enclosure (here represented by x), being evenly enclosed, can be erased by permission No 1, and then Permission No 4, which allows a double enclosure round any graph under even enclosures, permits the double enclosure to be removed under odd enclosures. I mean the double enclosure formed of the cut of the vacant enclosure together with the cut enclosing it. This done nothing but a blank remains; and so, within odd and even numbers of cuts alike, the whole enclosure containing the pseudograph may be suppressed. We thus get

Permission No 6. Any enclosure containing a blot or other pseudograph may [be] suppressed whether evenly or oddly enclosed.

The predication of the definitum concerning the definition may be regarded as giving the last Alpha Fundamental Permission.

Permission No 7. A vacant cut may be treated as a pseudograph.

These seven permissions being, however, somewhat confusing, I replace them by a compact little code which I call the three primary rules. It runs as follows:

I now pass to the beta part of the system of existential graphs. It is far more interesting and important than the alpha part but incomparably less so than the gamma part.

When one hears a proper name mentioned for the first time, one generally learns of the individual person or thing denoted by that name that it exists. It may, of course, be identified with a subject of force already well-known; but that will be exceptional. It will frequently be apparent that it is a thing quite different from any hitherto mutually recognized. In this case, it will make an addition to the universe of discourse, brought about by means of the assertion of a real relation of it to an object previously recognized. Sometimes, it will be doubtful whether it is one of the recognized subjects of force or not. But what I want to focus your attention upon is that at the first mention of a proper name, apart from any special information about its subject that may then be conveyed, the name merely tells us that something exists, that is, is a factor of the entire complexus of forces that we partly have known by experience. But at any subsequent mention of the proper name, though this assertion of existence is reiterated, yet that being know[n] already is of no importance. The importance of the name at all occurrences after the first is that it identifies what is mentioned with something we had heard of before.

If you bear in mind these characteristics of proper names, you will perceive that when lawyers and others use the letters A, B, C as a sort of improved relative pronouns, saying for example that if A owes B money and C owes A money, then B may “trustee” C for the debt (as you say in Massachusetts), these letters differ from new proper names only in the accidental circumstance that they are first introduced in the antecedent of a conditional proposition while proper names are first introduced in positive assertions. I call such improvised proper names selectives.

There is nothing to prevent our using the capital letters as such individual names, provided we distinguish the first replica by scribing it heavily or otherwise. I cannot say that this is a bad way; it serves the purpose of putting out of view confusing [trifles?]. But I do say that it requires rather complicated rules, and from every other point of view except that of putting unimportant circumstances out of view and convenience in printing, is usually inferior to another way of fulfilling the same purpose, which I proceed to describe.

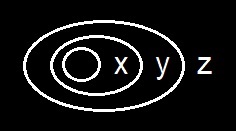
Since the blackboard, or the sheet of assertion, represents the universe of discourse, and since this universe is a collection of individuals, it seems reasonable that any decidedly marked point of the sheet should stand for a single individual; so that • should mean “something exists.” We cannot make this • • to mean that two things exist, since this would conflict with our convention that graphs on different parts of the sheet shall have each the same meaning as if each stood alone, so that consequently the second point merely reiterates that something exists.

You will ask me what use I propose to make of this sign that something exists, a fact that graphist and interpreter took for granted at the outset. I will show you that the sign will be useful as long as we agree that although different points on the sheet may denote the same individual, yet different individuals cannot be denoted by the same point on the sheet.

If we take any proposition, say

A sinner kills a saint
and if we erase portions of it, so as to leave it a blank form of proposition, the blanks being such that if every one of them is filled with a proper name, a proposition will result, such as
______ kills a saint
A sinner kills ______
______ kills ______
where Cain and Abel might for example fill the blanks, then such a blank form, as well as the complete proposition, is called a rheme (provided it be neither [by] logical necessity true of everything nor true of nothing, but this limitation may be disregarded). If it has one blank it is called a monad rheme, if two a dyad, if three a triad, if none a medad (from μηδέν).

Now such a rheme being neither logically necessary nor logically impossible, as a [part of ?] a graph without being represented as a combination by any of the signs of the system, is called a lexis and each replica of the lexis is called a spot. (Lexis is the Greek for a single word and a lexis in this system corresponds to a single verb in speech. The plural of lexis is preferably lexeis rather than lexises.)

Such a spot has a particular point on its periphery appropriated to each and every one of its blanks. Those points, which, you will observe, are mere places, and are not marked, are called the hooks of the spot. But if a marked point, which we have agreed shall assert the existence of an individual, be put in that place which is a hook of a graph, it must assert that some thing is the corresponding individual whose name might fill the blank of the rheme. Thus

• gives • to • in exchange for •
will mean “something gives something to something in exchange for something.”

Now let us further agree that a heavily marked line , all whose points are ipso facto heavily marked and therefore denote individuals, shall be a graph asserting the identity of all the individuals denoted by its points. Then

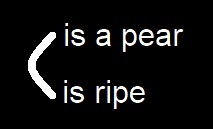
will mean that there is a ripe pear, that is, something is a pear and that very same thing is ripe.

We call such a heavy line a line of identity. A point from which three lines of identity proceed has the force of the conjunction ‘and.’

There is no need of a point from which four lines of identity proceed; for two triple points answer the same purpose.
Therefore a figure like this
is to be understood as two distinct lines of identity crossing one another. Nevertheless, in order to avoid possible mistake a bridge may be represented thus:
One line passes under the bridge, the other upon it.

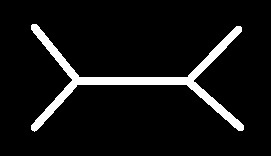
The more you scribe on the bottom of a cut, the less you assert. Thus

means: It is not true that somebody returns to earth nor is it true that somebody is translated. But
merely says that both are not true. That is one or [the] other is false. Either nobody returns to earth or else nobody is translated. Add to this a line of identity joining the two
and still less is asserted. Either nobody is translated or if anybody is translated, that person does not return to earth.

Now take this

That means somebody is a prophet but nobody is translated. If we continue the outer line to the cut, it will make no difference
for no significance attaches to the shape of the line. If, however, the inner line be extended to join the point on the cut, much less is asserted
This means: Somebody is a prophet and this person is not translated; that is Some prophet is not translated.

Lines of identity bring only one new rule of illative transformation. (Illative transformation, by the way, is transformation of the nature of necessary inference.) But lines of identity require some slight changes to be made in the three primary rules already given.

Under the rule of omission and insertion, it is to be noted that a line of identity may be broken within an even number of cuts or on the sheet of assertion, while two lines may be joined within an odd number of cuts. We also have the curious fact that as far as this rule is concerned a point on a cut is to be treated as being within the cut, although in other respects it is to be treated as being outside the cut. The cause of this is that we take it for granted that something exists. How this cause produces this effect I shall leave it for you to make out.

The rule about the double enclosure receives an extension since not only are two cuts of no effect when no graph is between them, but they are equally so when nothing is between them except lines of identity that [traverse?] the space between the two cuts.

The rule of iteration and deiteration takes a form which cannot easily be expressed without defining a new term, ligature.

[Namely, a line of identity is, as I have said, a graph and as such it cannot be part on one side of a cut and part on the other side. In the graph

there are two lines of identity. But their having a common point on the cut identifies the individuals they denote.]
The bracketed passage here is written on a separate, unnumbered page, and Peirce drew a line from this page to the facing page (numbered 27) to show where it was to be inserted, so that is where i have inserted it. This is a common occurrence in the manuscripts of Lowell 2 (R 455 and 456), but i have drawn attention to this instance because it is an interpretive principle which Peirce changed his mind about in his April 1906 address to the National Academy of Science (CP 4.579):

‘In a certain partly printed but unpublished “Syllabus of Logic,” which contains the only formal or full description of Existential Graphs that I have ever undertaken to give, I laid it down, as a rule, that no graph could be partly in one area and partly in another; and this I said simply because I could attach no interpretation to a graph which should cross a cut. As soon, however, as I discovered that the verso of the sheet represents a universe of possibility, I saw clearly that such a graph was not only interpretable, but that it fills the great lacuna in all my previous developments of the logic of relatives. For although I have always recognized that a possibility may be real, that it is sheer insanity to deny the reality of the possibility of my raising my arm, even if, when the time comes, I do not raise it; and although, in all my attempts to classify relations, I have invariably recognized, as one great class of relations, the class of references, as I have called them, where one correlate is an existent, and another is a mere possibility; yet whenever I have undertaken to develop the logic of relations, I have always left these references out of account, notwithstanding their manifest importance, simply because the algebras or other forms of diagrammatization which I employed did not seem to afford me any means of representing them. I need hardly say that the moment I discovered in the verso of the sheet of Existential Graphs a representation of a universe of possibility, I perceived that a reference would be represented by a graph which should cross a cut, thus subduing a vast field of thought to the governance and control of exact logic.’

The passage in the “Syllabus” to which Peirce refers is CP 4.406, where he gives it as a corollary to Convention V that ‘no line of identity can cross a cut.’ After 1906, Peirce apparently reverted to the rule given here in Lowell 2; for instance in MS L 231 (1911), p.13-14:
‘Every indivisible graph instance must be wholly contained in a single area. The line of identity may be regarded as a graph composed of any number of dyads “— is —” or as a single dyad. But it must be wholly in one area. Yet it may abut upon another line of identity in another area.’

The explanation which follows in MS L 231 (NEM 3.1, 164) is essentially the same as that in Lowell 2 (above). See also Roberts 1973, pp. 88 ff.
By a ligature is meant a line of identity together with all other lines of identity that have points in common with it. For example
means any man loves himself. It has four lines of identity, one attached to the monad spot “is a man,” two attached to the dyad spot loves and one joining the triple point to the inner cut. But all those make a single “ligature.” Now the reformed rule of iteration and deiteration is, that any partial graph, detached or attached, may be iterated within the same or additional cuts provided every line or hook of the iterated graph be attached in the new replica to identically the same ligatures as in the primitive replica; and if a partial graph be already so iterated it can be deiterated by the erasure of one of the replicas which must be within every cut that the replica left standing is within. For example, suppose we have these premisses:
We can iterate the two outside lines of identity within the outer cut, thus:
Within one enclosure we can join the two lines on each side, thus:
We can now deiterate “mother of”, thus:
We can now erase the two cuts which have nothing between them but lines of identity, thus:
We can now erase “mother of,” thus

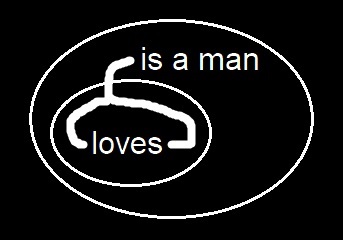
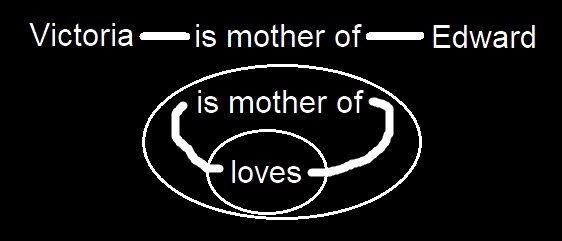
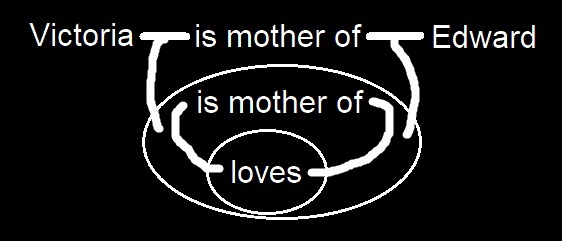
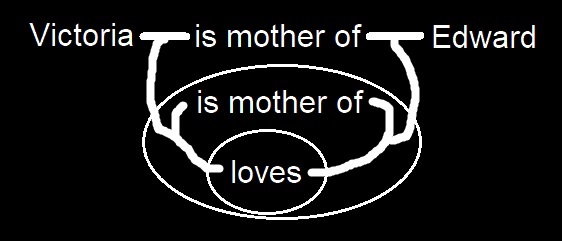
I now proceed to the new fourth rule. It runs as follows:

The innermost effective ligature between two spots lies within every cut that encloses both those spots.

In order to illustrate the meaning of this I take these [five] graphs:

The first three of these mean, respectively, “Nobody loves anybody whom he does not respect,” “Somebody loves nobody whom he does not respect,” “Somebody is loved by nobody who does not respect him.” Those three propositions cannot be expressed, with the same degree of analysis, without the ligature the innermost of which is within the cut that encloses both spots. But the fourth, which means “There is somebody whom somebody does not love unless he respects him” will not have its meaning changed by breaking both ligatures, as in the fifth graph, so as to make it read “Either there is somebody who non-loves somebody or else somebody respects somebody” or “If everybody loves everybody somebody respects somebody.[”] The juncture protruding through two cuts could be cut without altering the meaning:
By putting two cuts round the “loves” and retracting the junctures through two cuts we get the equivalent graph
The third chapter of the exposition of existential graphs is by far the most important and interesting of the three. The whole gist of mathematical reasoning depends upon it. I shall have to remit it to another [lecture.]



Lowell Lecture 3