Lowell Lecture 8 of 1903 (MS 475-6)

transcribed and edited by Gary Fuhrman, July-August 2018, from the manuscript copies made available by the SPIN project (link above). Parts of this lecture were previously published in CP 5.590-604. CP numbering is given here for those parts, but the text follows the manuscript (correcting a few errors in CP 5), with some punctuation altered for clarity.

The first two pages appear to be a draft of the introduction to the whole Lowell series, not to Lecture 8.

Ladies and Gentlemen:

For eight abbreviated hours I am to endeavor to occupy your attention with the subject of reasoning. But can one person inform another what is good reasoning and what is bad?

About seventy generations have passed since Aristotle gave to logic a scientific form. There has not been one of those generations in Europe that has not been occupied with this study and it is natural and proper to ask what the harvest has been. At the end of sixty of those seventy generations, Europeans reasoned no better than the personages of Plato's Dialogues are represented as reasoning. They were more considerably more adroit,— they reached their conclusions with greater facility; but the conclusions were neither more sure nor further-reaching; and as to the character of the reasoning, it was of a decidedly less vigorous and fecund kind than that of Plato himself. As for the science of logic, if remained substantially the very doctrine that Aristotle had taught.

Galileo inaugurated the science of dynamics about 1590, and his work was well-known and had its effect, although his book was not published for near half a century later; and it was the study of dynamics, more than anything else, which gradually taught men to reason better on all subjects. I do not say that it was the sole cause; for Tycho Brahe established his observatory half a dozen years before Galileo was appointed professor in Pisa; and the principle of our system of

The MS breaks off here; the next page is the title page of Lecture 8. These first three pages appear to be paperclipped in front of the rest of the lecture.

Ladies and Gentlemen:

The most prominent peculiarity of the system of logic which my studies have led me to adopt is that instead of being satisfied with the almost universal division of all reasoning into Necessary and Probable Reasoning, I find myself forced to recognize three grand branches,

Because this doctrine is almost peculiar to myself as yet, having only been preached by one obscure pen for only thirty or forty years, which is a short time in the development of such broad conceptions,— because of this, you will very naturally and properly be somewhat sceptical about it. In logic, however, authority is wholly out of place. We ought to suspend our judgment upon any logical questions until we thoroughly comprehend the matter, when we shall plainly see which answer is correct.

I will tell you how I became forced to this opinion. The first step was taken in consequence of studying the doctrine of probabilities, and especially Boole's treatment of that branch of logic in his volume entitled Laws of Thought. Now that book was written at a time when the clear ideas about all things mathematical that are today common to all real masters in mathematics, were just beginning to sprout, just making their appearance above the ground. That book of Boole's may well be compared to the De Revolutionibus of Copernicus. You know that the system of Copernicus, until Keppler came, met with considerable dissent on the part of those astronomers who were entirely neutral on the Biblical question. The reason was that although it contained one immense simplification which ought to have caused its acceptance, and would have done so if all astronomers had been reasoners of the highest order, yet owing to Copernicus not having the skill that Ptolemy had in framing hypotheses, the system, as it was set forth in his book, was just as complicated as the Ptolemaic system, if not more so. It was much the same with Boole's Laws of Thought. He took some steps in clearing up the conception of probability which could only be taken by a genius as sublime as his; but owing to his continuing to cling so some of the old phantoms, and especially to that of a “simple event,” his doctrine, on the whole, was perhaps even more confused than that of Laplace. But it is characteristic of the greatest minds, Aristotle, Scotus, Copernicus, Kant, Laplace, Boole, that even before they are able to extricate their ideas from confusion, they are already able to work with those ideas better than ordinary men can do after the ideas have been perfectly analyzed. At any rate, the study of that book made it perfectly clear to my mind that an inductive argument does not render its conclusion any more probable than it was before, using the word probable in the only sense that can give any real meaning to the doctrine of chances. An inductive argument does not increase the chances in favor of the truth of the proposition that it concludes. Indeed it is difficult to see what definite meaning can be attached to the phrase “the chances in favor of the truth of the proposition which induction infers.” If you could put all possible universes into a bag and after shaking them well up, would draw out universe after universe, you might form statistics as to the proportion of universes in which the proposition is true. But since you cannot do that, to speak of the probability of the truth of a general proposition, to speak, that is to say, of the statistical ratio of frequency with which in the future course of experience the proposition will be found true, leaves us at a loss to conjecture what the other term of that ratio can be meant to be. It thus became plain to me that induction is something radically different in its nature from deduction; and I was thus led to ask, What is induction? I endeavored to formulate the process syllogistically; and I found that it could be defined as the inference of the major premiss of a syllogism from its minor premiss and conclusion. Now this was exactly what Aristotle said it was in 23rd Chapter of the 2nd Book of the Prior Analytics, concerning which Grote is the best commentator. Aristotle's example is

CP 5.590 begins here.

590. if we are to give the names of Deduction, Induction, and Abduction to the three grand classes of inference, then Deduction must include every attempt at mathematical demonstration, whether it relate to single occurrences or to “probabilities,” that is, to statistical ratios; Induction must mean the operation that induces an assent, with or without quantitative modification, to a proposition already put forward, this assent or modified assent being regarded as the provisional result of a method that must ultimately bring the truth to light; while Abduction must cover all the operations by which theories and conceptions are engendered.

591. How is it that man ever came by any correct theories about nature? We know by Induction that man has correct theories; for they produce predictions that are fulfilled. But by what process of thought were they ever brought to his mind? A chemist notices a surprising phenomenon. Now if he has a high admiration of Mill's Logic, as many chemists have, he will remember that Mill tells him that he must work on the principle that, under precisely the same circumstances, like phenomena are produced. Why does he then not note that this phenomenon was produced on such a day of the week, the planets presenting a certain configuration, his daughter having on a blue dress, he having dreamed of a white horse the night before, the milkman having been late that morning, and so on? The answer will be that in early days chemists did use to attend to some such circumstances, but that they have learned better. How have they learned this? By an induction. Very well, that induction must have been based upon a theory which the induction verified. How was it that man was ever led to entertain that true theory? You cannot say that it happened by chance, because the possible theories, if not strictly innumerable, at any rate exceed a trillion,— or the third power of a million; and therefore the chances are too overwhelmingly against the single true theory in the twenty or thirty thousand years during which man has been a thinking animal, ever having come into any man's head. Besides, you cannot seriously think that every little chicken that is hatched has to rummage through all possible theories until it lights upon the good idea of picking up something and eating it. On the contrary, you think the chicken has an innate idea of doing this; that is to say, that it can think of this, but has no faculty of thinking anything else. The chicken you say pecks by instinct. But if you are going to think every poor chicken endowed with an innate tendency toward a positive truth, why should you think that to man alone this gift is denied? If you carefully consider with an unbiassed mind all the circumstances of the early history of science and all the other facts bearing on the question, which are far too various to be specifically alluded to in this lecture, I am quite sure that you must be brought to acknowledge that man's mind has a natural adaptation to imagining correct theories of some kinds, and in particular to correct theories about forces, without some glimmer of which he could not obtain food, and to correct theories about the human mind, without some glimmer of which he could not form social ties and consequently could not reproduce his kind. In short, the instincts conducive to assimilation of food, and the instincts conducive to reproduction, must have involved from the beginning certain tendencies to think truly about physics, on the one hand, and about psychics, on the other. It is somehow more than a mere figure of speech to say that nature fecundates the mind of man with ideas which, when those ideas grow up, will resemble their father, Nature.

592. But if that be so, it must be good reasoning to say that a given hypothesis is good, as a hypothesis, because it is a natural one, or one readily embraced by the human mind. It must concern logic in the highest degree to ascertain precisely how far and under what limitations this maxim may be held. For of all beliefs, none is more natural than the belief that it is natural for man to err. The logician ought to find out what the relation is between these two tendencies.

593. It behooves a man first of all to free his mind of those four idols of which Francis Bacon speaks in the first book of the Novum Organum. So much is the dictate of Ethics, itself. But after that, what? Descartes, as you know, maintained that if a man could only get a perfectly clear and distinct idea,— to which Leibniz added the third requirement that it should be adequate,— then that idea must be true. But this is far too severe. For never yet has any man attained to an apprehension perfectly clear and distinct, let alone its being adequate; and yet I suppose that true ideas have been entertained. Ordinary ideas of perception, which Descartes thought were most horribly confused, have nevertheless something in them that very nearly warrants their truth, if it does not quite so. “Seeing is believing,” says the instinct of man.

594. The question is what theories and conceptions we ought to entertain. Now the word “ought” has no meaning except relatively to an end. That ought to be done which is conducive to a certain end. The inquiry therefore should begin with searching for the end of thinking. What do we think for? What is the physiological function of thought? If we say it is action, we must mean the government of action to some end. To what end? It must be something good or admirable, regardless of any ulterior reason. This can only be the esthetically good. But what is esthetically good? Perhaps we may say the full expression of an idea? Thought, however, is in itself essentially of the nature of a sign. But a sign is not a sign unless it translates itself into another sign in which it is more fully developed. Thought requires achievement for its own development, and without this development it is nothing. Thought must live and grow in incessant new and higher translations, or it proves itself not to be genuine thought.

595. But the mind loses itself in such general questions and seems to be floating in a limitless vacuity. It is of the very essence of thought and purpose that it should be special, just as truly as it is of the essence of either that it should be general. Some writers have called the circle beautiful: but it has no features: it is expressionless. No curve can be very beautiful, because the thought it embodies is too meagre. But as curves go, bicyclic quartics are as a matter of fact pleasing; and I think the reason is that they have something of the perfect regularity of the circle, with a continuity of a kind which developes special features. Hogarth's line of beauty is the simplest case of a special feature, a singularity, as it is called by geometers, which the law of the continuity itself engenders, without destroying the continuity. All this may seem to be very foreign to logic, and perhaps it is so. Yet it illustrates the point that the valuable idea must be eminently fruitful in special applications, while at the same time it is always growing to wider and wider alliances.

596. Classical antiquity was far too favorable to the sort of concept that was

597. Auguste Comte, at the other extreme, would condemn every theory that was not “verifiable.” Like the majority of Comte's ideas, this is a bad interpretation of a truth. An explanatory hypothesis, that is to say, a conception which does not limit its purpose to enabling the mind to grasp into one a variety of facts, but which seeks to connect those facts with our general conceptions of the universe, ought, in one sense, to be verifiable; that is to say, it ought to be little more than a ligament of numberless possible predictions concerning future experience, so that if they fail, it falls. Thus, when Schliemann entertained the hypothesis that there really had been a city of Troy and a Trojan War, this meant to his mind among other things that when he should come to make excavations at Hissarlik he would probably find remains of a city with evidences of a civilization more or less answering to the descriptions of the Iliad, and which would correspond with other probable finds at Mycenae, Ithaca, and elsewhere. So understood, Comte's maxim is sound. Nothing but that is an explanatory hypothesis. But Comte's own notion of a verifiable hypothesis was that it must not suppose anything that you are not able directly to observe. From such a rule it would be fair to infer that he would permit Mr. Schliemann to suppose he was going to find arms and utensils at Hissarlik, but would forbid him to suppose that they were either made or used by any human being, since no such beings could ever be detected by direct percept. He ought on the same principle to forbid us to suppose that a fossil skeleton had ever belonged to a living ichthyosaurus. This seems to be substantially the opinion of M. Poincaré at this day. The same doctrine would forbid us to believe in our memory of what happened at dinnertime today. I have for many years been an adherent of what is technically called Common Sense in philosophy, myself; and do not think that my Tychistic opinions conflict with that position; but I nevertheless think that such theories as that of Comte and Poincaré about verifiable hypotheses frequently deserve the most serious consideration; and the examination of them is never lost time; for it brings lessons not otherwise so easily learned. Of course with memory would have to go all opinions about everything not at this moment before our senses. You must not believe that you hear me speaking to you, but only that you hear certain sounds while you see before you a spot of black, white, and flesh color; and those sounds somehow seem to suggest certain ideas which you must not connect at all with the black and white spot. A man would have to devote years to training his mind to such habits of thought, and even then it is doubtful whether it would be possible. And what would be gained? If it would alter our beliefs as to what our sensuous experience is going to be, it would certainly be a change for the worse, since we do not find ourselves disappointed in any expectations due to common sense beliefs. If on the other hand it would not make any such difference, as I suppose it would not, why not allow us the harmless convenience of believing in these fictions, if they be fictions? Decidedly we must be allowed these ideas, if only as cement for the matter of our sensations. At the same time, I protest that such permission would not be at all enough. Comte, Poincaré, and Karl Pearson take what they consider to be the first impressions of sense, but which are really nothing of the sort, but are percepts that are products of psychical operations, and they separate these from all the intellectual part of our knowledge, and arbitrarily call the first real and the second fictions. These two words real and fictive bear no significations whatever except as marks of good and bad. But the truth is that what they call bad or fictitious, or subjective, the intellectual part of our knowledge, comprises all that is valuable on its own account, while what they mark good, or real, or objective, is nothing but the pretty vessel that carries the precious thought.

598. I can excuse a person who has lost a dear companion and whose reason is in danger of giving way under the grief, for trying, on that account, to believe in a future life. I can more than excuse him because his usefulness is at stake, although I myself would not adopt a hypothesis, and would not even take it on probation, simply because the idea was pleasing to me. Without judging others, I should feel, for my own part, that that would be a crime against the integrity of the reason that God has lent to me. But if I had the choice between two hypotheses, the one more ideal and the other more materialistic, I should prefer to take the ideal one upon probation, simply because ideas are fruitful of consequences, while mere sensations are not so; so that the idealistic hypothesis would be the more verifiable, that is to say, would predict more, and could be put the more thoroughly to the test.

Upon this same principle, if two hypotheses present themselves, one of which can be satisfactorily tested in two or three days, while the testing of the other might occupy a month, the former should be tried first, even if its apparent likelihood is a good deal less.

599. It is a very grave mistake to attach much importance to the antecedent likelihood of hypotheses, except in extreme cases; because likelihoods are mostly merely subjective, and have so little real value, that considering the remarkable opportunities which they will cause us to miss, in the long run attention to them does not pay. Every hypothesis should be put to the test by forcing it to make verifiable predictions. A hypothesis on which no verifiable predictions can be based should never be accepted, except with some mark attached to it to show that it is regarded as a mere convenient vehicle of thought,— a mere matter of form.

600. In an extreme case, where the likelihood is of an unmistakably objective character, and is strongly supported by good inductions, I would allow it to cause the postponement of the testing of a hypothesis. For example, if a man came to me and pretended to be able to turn lead into gold, I should say to him, “My dear sir, I haven't time to make gold.” But even then the likelihood would not weigh with me directly, as such, but because it would become a factor in what really is in all cases the leading consideration in Abduction, which is the question of Economy,— Economy of money, time, thought, and energy.

601. It is Prof. Ernst Mach who has done the most to show the importance in logic of the consideration of Economy, although I had written a paper on the subject as early as 1878. But Mach goes altogether too far. For he allows thought no other value than that of economizing experiences. This cannot for an instant be admitted. Sensation, to my thinking, has no value whatever except as a vehicle of thought.

602. Proposals for hypotheses inundate us in an overwhelming flood, while the process of verification to which each one must be subjected before it can count as at all an item even of likely knowledge is so very costly in time, energy, and money,— and consequently in ideas which might have been had for that time, energy, and money, that Economy here would override every other consideration even if there were any other serious considerations. In fact there are no others. For abduction commits us to nothing. It merely causes a hypothesis to be set down upon our docket of cases to be tried.

603. I shall be asked, Do you really mean to say that we ought not to adopt any opinion whatever as an opinion until it has sustained the ordeal of furnishing a prediction that has been verified?

In order to answer that question, it will be requisite to inquire how an abduction can be justified, here understanding by abduction any mode or degree of acceptance of a proposition as a truth because a fact or facts have been ascertained whose occurrence would necessarily or probably result in case that proposition were true. The abduction so defined amounts, you will remark, to observing a fact and then professing to say what idea it was that gave rise to that fact. One would think a man must be privy to the counsels of the Most High so to presume. The only justification possible, other than some such positive fact which would put quite another color upon the matter, is the justification of desperation. That is to say, that if he is not to say such things, he will be quite unable to know anything of positive fact.

In a general way, this justification certainly holds. If man had not had the gift, which every other animal has, of a mind adapted to his requirements, he not only could not have acquired any knowledge, but he could not have maintained his existence for a single generation. But he is provided with certain instincts, that is, with certain natural beliefs that are true. They relate in part to forces, in part to the action of minds. The manner in which he comes to have this knowledge seems to me tolerably clear. Certain uniformities, that is to say certain general ideas of action, prevail throughout the universe, and the reasoning mind is himself a product of this universe. These same laws are thus, by logical necessity, incorporated in his own being. For example, what we call straight lines are nothing but one out of an innumerable multitude of families of topically nonsingular lines such that through any two points there is one and one only. The particular family of lines called straight has no geometrical properties that distinguish it from any other of the innumerable families of lines of which there is one and one only through any two points. It is a law of dynamics that every dynamical relation between two points, no third point being concerned, except by combinations of such pairs, is altogether similar except in quantity to every such dynamical relation between any other two points on the same ray, or straight line. It is a consequence of this that a ray or straight line is the shortest distance between two points; whence, light appears to move along such lines; and that being the case, we recognize them by the eye, and call them straight. Thus, the faculty of sight naturally causes us to assign great prominence to such lines; and thus when we come to form a hypothesis about the motion of a particle left uninfluenced by any other, it becomes natural for us to suppose that it moves in a straight line. The reason this turns out true is, therefore, that this first law of motion is a corollary from a more general law which, governing all dynamics, governs light, and causes the idea of straightness to be a predominant one in our minds.

604. In this way, general considerations concerning the universe, strictly philosophical considerations, all but demonstrate that if the universe conforms, with any approach to accuracy, to certain highly pervasive laws, and if man's mind has been developed under the influence of those laws, it is to be expected that he should have a natural light, or light of nature, or instinctive insight, or genius, tending to make him guess those laws aright, or nearly aright. This conclusion is confirmed when we find that every species of animal is endowed with a similar genius. For they not only, one and all, have some correct notions of force, that is to say, some correct notions, though excessively narrow, of phenomena which we, with our broader conceptions, should call phenomena of force, and some similarly correct notions about the minds of their own kind and of other kinds, which are the two sufficient cotyledons of all our science, but they all have, furthermore, wonderful endowments of genius in other directions. Look at the little birds, of which all species are so nearly identical in their physique, and yet what various forms of genius do they not display in modelling their nests? This would be impossible unless the ideas that are naturally predominant in their minds were true. It would be too contrary to analogy to suppose that similar gifts were wanting to man. Nor does the proof stop here. The history of science, especially the early history of modern science, on which I had the honor of giving some lectures in this hall some years ago, completes the proof by showing how few were the guesses that men of surpassing genius had to make before they rightly guessed the laws of nature.

CP 5.604 ends here.

When we pass from considering the most general laws to more special ones,— say for example the laws of electricity,— the direct light of nature becomes dimmed; but then it is here replaced, in great measure, by analogies as to general characteristics of other laws already known.

Finally, we have to consider quite special hypotheses, such as the hypotheses which we make about ancient history. My time is now drawing to a close. I must cut off general explanations and will show by an example how I would treat a doubtful question of history.

On five occasions in my life, and on five occasions only, I have had an opportunity of testing my Abductions about historical facts, by the fulfillment of my predictions in subsequent archeological or other discoveries; and on each one of those five occasions my conclusions which in every case ran counter to that of the highest authorities, turned out to be correct. The two last cases were these. Prof. Petrie published a history of Egypt in which he treated the first three dynasties as mythical. I was just about writing a history of science and in the first chapter I showed why those Dynasties, including the name of Menes and other facts, ought to be considered historical. Before my book was near completed Petrie himself found the tomb of Menes. Again a few years ago I wrote in the Nation, where there was no room for details, that the Babylonians had high scientific genius and that there was reason to conjecture that Alexander sent home a Babylonian celestial globe dating from 2300 years B.C. Now the newest finds show that at that very date they were accomplished astronomers. You will find a specimen of my logical procedure in such a case in the __ volume of Science, where I discuss the Age of Basil Valentine. But in that case, I reach what may be counted as a certainty. In order to illustrate Abduction under difficulties, I want a case where the evidence is extremely slight and where the testimonies are open to grave suspicion, so that we cannot make the most distant approach to certainty in any way. I can think of no question that will answer this purpose better than the life of Pythagoras. Here I can only make a conjecture which I predict that future discoveries will confirm in its main features as far as those discoveries shall go. This theory will make no pretension to being knowledge, but only to being a good guess, which we may strongly and confidently hope will be confirmed.

[marginal note: “Here let those go who have to go”]

Almost all our information about Pythagoras comes from three writers who lived some five hundred years later. Just think what that means! Two of these three writers are known otherwise to be about as careless as any in that uncritical age. The third, who is the principal witness, is a superstitious romancer who sets forth supernatural narratives as simple historical fact. I mean Iamblichus. Moreover, as far as we can descry from what the modern histories of ancient philosophy say, there is no prospect of any hypothesis about Pythagoras ever being brought to the test. What, then, are we to do? We must take the different statements which we find in different ancient writers, the earliest of whom lived a century later, as facts. I do not mean that what they say is fact, but their saying so is a fact, and we must seek some rational explanation of how these facts came to be as they are. One of my chief maxims in such work is that you must never content yourself with saying, this witness knew nothing about it and therefore I do not believe what he says, or what this witness says is utterly impossible. That is no way to search out these things. You must have some definite and rational theory of how the witness was led to assert the particular untruth he does assert,— supposing it to be untruth. You must take that hypothesis which best unifies all the facts,— the facts that such and such assertions have been made by such and such writers; and that is the best conjecture possible. That is as near the truth as it is possible at present to come.

The least uncertain date in the life of Pythagoras is that he went to Italy at the age of forty in the year 532 B.C. So says Cicero, who was a very careful man. Less precisely Aulus Gellius and Iamblichus say the same. Sundry other authorities support the date by assertions that harmonize well with it. Let us begin the building of our hypothesis, then, by supposing that Pythagoras reached Italy in the summer of 532 B.C. It would necessarily be summer, owing to the conditions of navigation at that time. The most serious contradiction of this date is by the great historian Livy, who seems to say that Pythagoras came during the reign of Servius Tullius who was assassinated two years before. However, on carefully examining the passage of Livy, we remark that the historian only mentions this date in order to refute a statement by another historian that Numa Pompilius, the second king, had been aided by Pythagoras. Therefore Livy allows his adversary the earliest date ever assigned for the coming of Pythagoras. Thus the authority of the great historian is not against our date. But it was merely that some author had said something from which it might be inferred that Pythagoras might have come as early as Servius Tullius. We are obliged according to my rules to form some definite conjecture as to what was said. We may therefore suppose that the original authority said that Pythagoras came early in the third century of the city, or that he said he was seen on his arrival by some person of Servius Tullius's time. The assertion that Pythagoras aided Numa unfortunately yields no information because it needs no explanation, since it was quite inevitable that that assertion should be made, considering the ways of thinking of ancient writers. For Numa, they would say, must have been aided by some great political genius. For unless he was himself a great political sage he could not otherwise have made his laws; and if he was such a sage he certainly would have sought all the counsel he could get. Now no such adviser of Numa is mentioned. He must have been famous. But the only famous political genius of those days except Numa himself was Pythagoras. That is the way some writer of Livy's time would inevitably reason; for that is the very style of their thought. So the assertion was bound to get made irrespective of any facts. Consequently, it sheds no light at all on our subject.

All the witnesses are unanimous that Pythagoras having once arrived in Italy, passed all the rest of his life there. That too, then, we must accept, whether it seems likely or not. For we have no facts to go upon but the facts that assertions have been made by those writers; and there is no way of explaining the fact that one and all represent Pythagoras to have passed all the rest of his life in Italy except by supposing he really did so.

In particular Iamblichus expressly says so. But now we meet with a singular, and therefore a significant fact. It is that Iamblichus asserts that Pythagoras was taken prisoner by Cambyses in Egypt and was carried off to Babylon. But Cambyses was not in Egypt until 527 B.C., [????] four or five years after Pythagoras had settled in Crotona,— Croton. This, then, is plainly impossible; and the method of the German higher critics,— I do not speak only of such extravagant critics as the very learned Rose, but of such temperate critics as the highly esteemed Zeller,— is, having shown the assertion to be false, to cast it aside as worthless. That is very illogical; for false assertions are frequently far more significant than true ones. The question is, How are we to explain this assertion of Iamblichus.

Now it is a fact beyond all doubt that Pythagoras established a secret brotherhood In Italy. Its secrets were remarkably well kept for three hundred years and more. The secrets which history shows are the best kept among associations of men are trade-secrets, and since the Pythagoreans seem to have supported themselves, it is likely that their secrets comprised some knowledge that would enable its possessors to do something from which they could gain their living. Please bear that in mind, although we have no immediate need of it. The point we have need [of] is that during the five centuries which elapsed from the establishment of this brotherhood by Pythagoras to the time when the brotherhood decided to make public some facts about Pythagoras in order to fill up their numbers, as we know they must have done from the fact that then for the first time 3 Pythagoreans almost contemporaneously published biographies of their great master, this brotherhood remained most closely bound together with a worship of Pythagoras as a supernatural person and communicated by word of mouth exclusively. They therefore must have had a tradition about their master in which the supernatural elements were exaggerated but which in other respects was very close to the truth, as compared with traditions generally. Now in our days it has been clearly established that traditions generally, when unmixed with poetry, are apt to be pretty close to the truth in their main features. Iamblichus belonged to this brotherhood himself, and though he was a careless and highly superstitious writer, incapable of putting two and two together, and all the more valuable witness on that account, yet he depended very largely for his facts upon another life of Pythagoras by a somewhat earlier member of the brotherhood who was evidently much more careful; although for some reason, which I have not sufficiently reflected upon, his biography was not deemed sufficient and has been lost to us. Under these circumstances, how shall we explain the evidently false assertion of Iamblichus that Pythagoras was taken prisoner by Cambyses in Egypt?

Of course Iamblichus would be familiar with the fact [that] Pythagoras had been in Egypt. The German higher critics never evinced their marvellous genius for blundering more than when they have cast a certain doubt on this fact, which is not only testified to by every writer from Plato down who ever uttered the name of Pythagoras, so that to this day, if a child asks its mamma who Pythagoras was, the first or second sentence of the reply will mention his being a great traveller. And aside from all testimony, it is a priori certain that Pythagoras would go to Egypt. For in the relative state of culture of Ionia where he was born in the island of Samos,— and Egypt, it is certain that any youth desirous of a superior education would go to Egypt, if he could afford it, as Pythagoras evidently could. Far more certain than it is today that any American doctor of philosophy has studied in Germany. Pythagoras, however, was renowned for his extensive travels. Egypt would be the very first country he would visit. Iamblichus, then, was familiar with that fact; and also knew of the famous conquest of Egypt by Cambyses. One might more easily be ignorant today of the massacre of St. Bartholemew. His assertion shows that he had often heard among his Pythagorean brethren that Pythagoras had been taken prisoner by the Persians, and had been carried into captivity. How are we to explain the existence of such a tradition in that brotherhood? The obvious explanation is that Pythagoras really had been taken prisoner by the Persians and carried into captivity. We see that it could not have been by Cambyses. On what occasion could it have been? There is only one way in which it could have happened. Namely when Cyrus in 546 B.C. conquered Lydia. At no other time in the life of Pythoagoras did the Persians come near the Greek world. But is it reasonable to suppose that Pythagoras could have been in Lydia at that time? Why, all the witnesses say [that] Pythagoras was the son and heir of a wealthy merchant of Samos. The only reasonable explanation of that is that he really was so. Now Samos is right off the coast of Lydia in sight of the mainland. The son of a wealthy merchant of Samos would in all probability have interests in Lydia, both financial and sentimental. He would be specially likely to be there in times of trouble. It is, therefore, a particularly reasonable conjecture that it was then and there that Pythagoras was taken prisoner by the Persians, for it must have been then and there or never and nowhere. So, then, we will suppose, with great confidence, that this is what did take place; and it perfectly explains the assertion of Iamblichus who would most likely have forgotten this temporary invasion which occurred five centuries before he wrote. Having in his mind the fact that Pythagoras had been in Egypt, that he was captured by the Persians, and that Cambyses, the general of Cyrus, conquered Egypt, it was most natural that in the loose way that is eminently characteristic of him he would have put these things together as he did.

However, we must not miss any opportunity of putting the elements of our conjecture to the test during the process of constructing it; and therefore since this supposition that Pythagoras was taken prisoner by Cyrus involves a date, we must inquire whether or not that date fits in to all our other information. Now Iamblichus says that Pythagoras remained away for 12 years. When he got back to Samos he found that Polycrates had seized the government of the island. Now we otherwise know that such an event did take place about that time but the exact date of it is unsettled. There is some testimony that Pythagoras had been well-acquainted with Polycrates if not a friend of his. The testimony is of the very worst character possible. Namely, it is in the form of an ancient letter supposed to have been written by Pythagoras to Polycrates. I ought to explain why such testimony is so very bad, and why, at the same time, such false testimony is often of extreme value. You must know, then, if you do not already know it, that after the death of Alexander, Ptolemy Philadephus founded the Alexandrian library, and some of his successors became bitten with a perfect mania for perfecting that library, and spent enormous sums upon it, just as we see that bibliomaniacs do to this day. Only they exercized the force of their soldiery to increase the library by means of downright robbery, when purchases could not be made. The natural consequence of this was that there sprang up a regular business of forging books, on the one hand, and a critical art of detecting forgeries on the other hand. To forge a book was not easy. The Greeks, with slaves to do all their drudgery even of an intellectual kind, polished their writings to a point almost inconceivable to us; and to imitate a great literary writer in any long piece was quite impossible,— although philosophers might be imitated. But with a short letter, the case was different. All the forger had to do was to inform himself minutely of all that was to be known of a certain situation of a famous man and he could produce a letter which the librarians in Alexandria, while not perhaps fully believing in it, might yet not be willing to assume the responsibility of rejecting. In that way, a good many letters have come down to us, the great majority of which are doubtless spurious, and contain matter of fact purely imaginary; and yet having been written with sufficient skill to baffle the by no means unintelligent critics attached to the library, they have a great deal of real historical truth of a more or less general kind valuable to us, interwoven with their fictions.

It is likely that Pythagoras and Polycrates, both very superior men living on the small island of Samos together, would be acquainted with one another. At any rate, the story goes that Pythagoras, returning to Samos, found Polycrates in power, that he did not like this state of things, and that he sold out all his possessions and betook himself to Italy. So, then, after he returned to Samos, there would be first a period during which his discontent was growing to the point of causing his resolve to emigrate. Next there would be a period during which he was disposing of his varied possessions and deciding whither he would go. Having decided, he would have to wait for summer before he couold go. Two years seems to be the most reasonable period to allow a man like Pythagoras to go through all this. It cannot be much too long or much too short. Add that to the 12 years that Iamblichus says he was away, and we have 14 which precisely carries us from 546 B.C. when he was captured to 532 B.C. when he appeared in Italy. This is highly favorable to our supposition.

But let us trace out its consequences a little further. We must always push our hypotheses to their remotest consequences; and it is only when we find them always fitting into the facts that we can begin positively to believe in them.

Iamblichus says that Pythagoras was carried to Babylon. So he doubtless would have been if he had been taken prisoner by Cambyses, Babylon being the capital of the Persian empire. But Cyrus did not subdue Babylon until 538 B.C., and therefore in 546 B.C. Pythagoras could not have been carried there. But being by all odds the most distinguished person whom Cyrus had taken excepting Croesus himself, he would, beyond a doubt, have been carried by Cyrus where Cyrus himself went. Where did Cyrus go then? He went to Ecbatana.

But stop a bit! Let us reflect upon that. Babylon in those days was still the great centre of science and of philosophy. If Pythagoras went to Babylon his doctrine would surely be saturated with Babylonian ideas. At Ecbatana we do not know exactly what the local influences would have been;— probably not of any very powerful kind. He would have been influenced,— and perhaps we may say chiefly influenced by the Persian magi that Cyrus would have had there, whose ruling idea was a dualism of good and evil. Now how is it, in fact? The fact is that dualism is the most prominent feature of what we know of the philosophy of Pythagoras; and the careful Cicero, as well as others independently of Cicero, tell us that Pythagoras had personal relations with Persian magi.

There is not a trace of Babylonian science in the doctrine of Pythagoras. That is, indeed, what most marks him off from all the other philosophers of Greece, and sets him into a class of his own. For Greece was soon to become largely under the intellectual sway of Babylon, at least in scientific matters. Her astronomy for example was derived from Babylon; but the Pythagorean astronomy was entirely different. Astrology came from Babylon; but the Pythagoreans, inclined as they were to such mystical doctrines, were never astrologers. Babylon was above all things given to magic, that is to exorcisms of spirits. But there are no traces of [this?] among the Pythagoreans. Babylonian weights and measures, the Babylonian division of the circle, became naturalized in Greece; but in the cities where Pythagorean ideas prevail we find nothing of these. The theory of some writers that Pythagoras contributed to their introduction into Greece is perfectly gratuitous. Much secrecy hangs over the Pythagorean arithmetic, which was partly scientific and partly mystical. But no such ideas came from Babylon. The Pythagoreans held to metempsychosis, but the Babylonians knew nothing of it. The Hebrew scriptures are full of Babylonian influence; but there is nothing there like Pythagorean doctrine, unless it be the Cabbala. On the whole it is quite incredible that Pythagoras was for any long time in Babylon. The assertion of Eusebius that Pythagoras was influenced by the Chaldean wise men can therefore be an inference from his supposed long residence in Babylon. So here again our conjecture is confirmed.

Pythgoras, then, was carried to Ecbatana; and there, of course, he was a slave. Upon that there can be no shadow of doubt. Let us ask, then, would slavery suit the disposition of Pythagoras? The answer is that everything we are told of him shows him to have been an excessively dominating spirit. One might as well imagine Napoleon Bonaparte a slave. It is certain, then, that he would seek to escape, and that by the most feasible route. What, then, would be the most feasible and intelligent road of escape for a runaway in those days? It would not be to the south; for that would take him to the heart of Persia or to Babylon. It would not be to [the] west, for so he would have had to traverse the entire empire. It could not be to the north; for that way there was only the Caspian Sea and the impassible Caucausus. But just to the east was the frontier. To the east, then, he must have gone; since in fact he did get home. For the ideas of his being liberated or ransomed are too preposterous to be entertained. He must have gone east. And by what route? No doubt by the very road that Alexander two centuries later found to be the best. In fact, it was the only road. In any other direction eastward was the great desert. Eastward, then, he certainly did go. Where would that road take him? Certainly to Arya, that country after which we call our supposed race, the Aryans. What route he would have gone from there is not quite so evident. Alexander here turned to the south and after penetrating the desert was obliged to turn back again. However, one thing is certain; Pythagoras must in some way have got down through Afghanistan and Beluchistan to the mouth of the Indus and must there have taken passage home by way of Suez. All this is absolutely forced upon us from the moment that we assent to the proposition that Pythagoras was captured by the Persians.

There are some further consequences to be drawn from the supposed fact of this journey. Pythagoras never could have accomplished his escape without help. He must have sought it. He must have sought sympathy. Sympathy and help he would and (without a doubt I say it) did find among the very men whom he would naturally have desired to become acquainted with, the priests and the philosophers. In Aria he would have found Brahmins. Now Clemens and several other authorities inform us that he did derive some of his doctrines from the Brahmins. The German higher critics have denied this. They naturally would, because their grand principle of criticism is that whatever your only witnesses say is false. They seek to reconstruct ancient history in defiance of all the testimony out of the ????ei? of an inhabitant of a German university town. But Dr. L. von Schroeder, the eminent Sanskritist, has proved pretty conclusively that there are half a dozen features of the Pythagorean doctrine which can have had no other origin than a Brahminical origin. There is one consequence more; pretty doubtful I admit, yet worth taking into account. That region about Aria has a remarkable connection with a great fact of our intellectual history, since it is there that we find the first traces of what we call the Arabic system of numerical notation. The first four figures are said to be nothing else than the initials of the names of the first four numbers in an alphabet found in that region. The old name for vulgar arithmetic in Chaucer, mentioned also in Recorde's Grounde of Artes, the earliest arithmetic in the English language, is augrim. Now this word “augrim” is nothing but the corruption of Al-Kwarizmi, which means the man [of] Chorasmia, being the surname of the mathematician who originally introduced our vulgar arithmetic to the Arabians. It was not original with him, but was commonly used in Chorasmia, which is a country north of Aria. There is no evidence at all that the socalled Arabic system was in use even in Aria much before the christian era; but likely enough that it was so. The cipher for naught would probably not then have been in use. For the system was originally only used for calculations made in ruled columns. The figures were not written as a substitute for the name of the number. As long as the use of it was restricted to computations, the absence of the cipher would be a matter of no consequence. If the system was used in Aria for calculations at that early day, we may be tolerably sure that Pythagoras would become acquainted with it. We know that the Pythagorean brethren, who were highly refined, exclusive, gentlemanly, and aristocratic people, supported themselves for centuries by their brains, and that they possessed some secret about numbers,— which was kept as only trade secrets are apt to be kept,— and which secret was of such a nature as to lead them to speak in concealed ways of the number ten. Thus they called it the tetrad, a word which does not naturally suggest ten; but ten was called the tetrad because of the figure

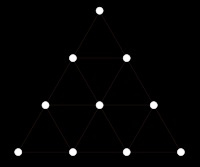
Perhaps the Pythagoreans supported themselves by book-keeping, by making computations as many Italians did at a much later day. We only know that in a book of Boethius, who lived about A.D. 500, the Arabic figures are given and are said to be used by the Pythagoreans. It is true that the critics have endeavored to make it probable, or to use their favorite expression to “demonstrate”,— some of them that this chapter of the book is spurious, others that the whole of the second book of the Geometry of Boethius in which this chapter occurs is spurious, still others that the entire work is spurious. But it never seems to have occurred to any of them that even if they were to prove it spurious, which they are very far from having done, it would still remain to be explained how this very singular passage ever came to be written at all or ever came to be attributed to Boethius. For my part, having most carefully examined all the evidence and several of the manuscripts, I have no doubt at all that the passage is genuine. I consider the arguments brought against it to be utter rubbish. I have thus run through the almost necessary consequences of explaining the assertion by Iamblichus that Pythagoras was taken prisoner by the Persians under Cambyses by supposing it due to the fact that he had been taken prisoner by the Persians under Cyrus. You have seen how the consequences fit into fact and have, I hope, been impressed with the necessity of explaining testimonies whether they be true or whether, as in this case, they be false.