C.S. Peirce: Prolegomena to an Apology for Pragmaticism

The Monist, pp. 492-546, vol. 16 (1906), with some minor corrections as listed in vol. 17, p. 160. Text as in CP 4.530-572 except for a few corrections, and omitting section divisions and footnotes inserted by CP editors). Peirce's own notes are given here in the text, immediately after the sentence to which they apply, in a slightly smaller font size.
For Peirce's own extended comments on this text, see “The Bed-Rock Beneath Pragmaticism” (early 1908).

530. Come on, my Reader, and let us construct a diagram to illustrate the general course of thought; I mean a System of diagrammatization by means of which any course of thought can be represented with exactitude.

“But why do that, when the thought itself is present to us?” Such, substantially, has been the interrogative objection raised by more than one or two superior intelligences, among whom I single out an eminent and glorious General.

Recluse that I am, I was not ready with the counter-question, which should have run, “General, you make use of maps during a campaign, I believe. But why should you do so, when the country they represent is right there?” Thereupon, had he replied that he found details in the maps that were so far from being “right there,” that they were within the enemy's lines, I ought to have pressed the question, “Am I right, then, in understanding that, if you were thoroughly and perfectly familiar with the country, as, for example, if it lay just about the scenes of your childhood, no map of it would then be of the smallest use to you in laying out your detailed plans?” To that he could only have rejoined, “No, I do not say that, since I might probably desire the maps to stick pins into, so as to mark each anticipated day's change in the situations of the two armies.” To that again, my sur-rejoinder should have been, “Well, General, that precisely corresponds to the advantages of a diagram of the course of a discussion. Indeed, just there, where you have so clearly pointed it out, lies the advantage of diagrams in general. Namely, if I may try to state the matter after you, one can make exact experiments upon uniform diagrams; and when one does so, one must keep a bright lookout for unintended and unexpected changes thereby brought about in the relations of different significant parts of the diagram to one another. Such operations upon diagrams, whether external or imaginary, take the place of the experiments upon real things that one performs in chemical and physical research. Chemists have ere now, I need not say, described experimentation as the putting of questions to Nature. Just so, experiments upon diagrams are questions put to the Nature of the relations concerned.” The General would here, may be, have suggested (if I may emulate illustrious warriors in reviewing my encounters in afterthought), that there is a good deal of difference between experiments like the chemist's, which are trials made upon the very substance whose behavior is in question, and experiments made upon diagrams, these latter having no physical connection with the things they represent. The proper response to that, and the only proper one, making a point that a novice in logic would be apt to miss, would be this: “You are entirely right in saying that the chemist experiments upon the very object of investigation, albeit, after the experiment is made, the particular sample he operated upon could very well be thrown away, as having no further interest. For it was not the particular sample that the chemist was investigating; it was the molecular structure. Now he was long ago in possession of overwhelming proof that all samples of the same molecular structure react chemically in exactly the same way; so that one sample is all one with another. But the object of the chemist's research, that upon which he experiments, and to which the question he puts to Nature relates, is the Molecular Structure, which in all his samples has as complete an identity as it is in the nature of Molecular Structure ever to possess. Accordingly, he does, as you say, experiment upon the Very Object under investigation. But if you stop a moment to consider it, you will acknowledge, I think, that you slipped in implying that it is otherwise with experiments made upon diagrams. For what is there the Object of Investigation? It is the form of a relation. Now this Form of Relation is the very form of the relation between the two corresponding parts of the diagram. For example, let f[1] and f[2] be the two distances of the two foci of a lens from the lens. Then,

This equation is a diagram of the form of the relation between the two focal distances and the principal focal distance; and the conventions of algebra (and all diagrams, nay all pictures, depend upon conventions) in conjunction with the writing of the equation, establish a relation between the very letters f₁, f₂, f₀ regardless of their significance, the form of which relation is the Very Same as the form of the relation between the three focal distances that these letters denote. This is a truth quite beyond dispute. Thus, this algebraic Diagram presents to our observation the very, identical object of mathematical research, that is, the Form of the harmonic mean, which the equation aids one to study. (But do not let me be understood as saying that a Form possesses, itself, Identity in the strict sense; that is, what the logicians, translating ἀριθμῷ, call ‘numerical identity.’)”

531. Not only is it true that by experimentation upon some diagram an experimental proof can be obtained of every necessary conclusion from any given Copulate of Premisses, but, what is more, no “necessary” conclusion is any more apodictic than inductive reasoning becomes from the moment when experimentation can be multiplied ad libitum at no more cost than a summons before the imagination. I might furnish a regular proof of this, and am dissuaded from doing so now and here only by the exigency of space, the ineluctable length of the requisite explanations, and particularly by the present disposition of logicians to accept as sufficient F. A. Lange's persuasive and brilliant, albeit defective and in parts even erroneous, apology for it. Under these circumstances, I will content myself with a rapid sketch of my proof. First, an analysis of the essence of a sign, (stretching that word to its widest limits, as anything which, being determined by an object, determines an interpretation to determination, through it, by the same object), leads to a proof that every sign is determined by its object, either first, by partaking in the characters of the object, when I call the sign an Icon; secondly, by being really and in its individual existence connected with the individual object, when I call the sign an Index; thirdly, by more or less approximate certainty that it will be interpreted as denoting the object, in consequence of a habit (which term I use as including a natural disposition), when I call the sign a Symbol.^nP

532. But since you may, perhaps, be puzzled to understand how an Icon can exhibit a necessity — a Must-be — I will here give, as an example of its doing so, my proof that the single members of no collection or plural, are as many as are the collections it includes, each reckoned as a single object, or, in other words, that there can be no relation in which every collection composed of members of a given collection should (taken collectively as a single object) stand to some member of the latter collection to which no other such included collection so stands. This is another expression of the following proposition, namely: that, taking any collection or plural, whatsoever, be it finite or infinite, and calling this the given collection; and considering all the collections, or plurals, each of which is composed of some of the individual members of the given collection (but including along with these Nothing which is to be here regarded as a collection having no members at all; and also including the single members of the given collection, conceived as so many collections each of a single member), and calling these the involved collections; the proposition is that there is no possible relation in which each involved collection (considered as a single object), stands to a member of the given collection, without any other of the involved collections standing in the same relation to that same member of the given collection. This purely symbolic statement can be rendered much more perspicuous by the introduction of Indices, as follows. The proposition is that no matter what collection C may be, and no matter what relation R may be, there must be some collection, c', composed exclusively of members of C, which does not stand in the relation R to any member, k, of C, unless some other collection, c'', likewise composed of members of C, stands in the same relation R to the same k. The theorem is important in the doctrine of multitude, since it is the same as to say that any collection, no matter how great, is less multitudinous than the collection of possible collections composed exclusively of members of it; although formerly this was assumed to be false of some infinite collections. The demonstration begins by insisting that, if the proposition be false, there must be some definite relation of which it is false. Assume, then, that the letter R is an index of any one such relation you please. Next divide the members of C into four classes as follows:

Class I is to consist of all those members of C (if there be any such) to each of which no collection of members of C stands in the relation R.

Class II is to consist of all those members of C to each of which one and only one collection of members of C stands in the relation R; and this class has two subclasses, as follows:

Sub-Class 1 is to consist of whatever members of Class II there may be, each of which is contained in that one collection of members of C that is in the relation R to it.

Sub-Class 2 is to consist of whatever members of Class II there may be, none of which is contained in that one collection of members of C that is in the relation R to it.

Class III is to consist of all those members of C, if there be any such, to each of which more than one collection of members of C are in the relation R.

This division is complete; but everybody would consider the easy diagrammatical proof that it is so as needless to the point of nonsense, implicitly relying on a Symbol in his memory which assures him that every Division of such construction is complete.

I ought already to have mentioned that, throughout the enunciation and demonstration of the proposition to be proved, the term “collection included in the given collection” is to be taken in a peculiar sense to be presently defined. It follows that there is one “possible collection” that is included in every other, that is, which excludes whatever any other excludes. Namely, this is the “possible collection” which includes only the Sphinxes, which is the same that includes only the Basilisks, and is identical with the “possible collection” of all the Centaurs, the unique and ubiquitous collection called “Nothing,” which has no member at all. If you object to this use of the term “collection,” you will please substitute for it, throughout the enunciation and the demonstration, any other designation of the same object. I prefix the adjective “possible,” though I must confess it does not express my meaning, merely to indicate that I extend the term “collection” to Nothing, which, of course, has no existence. Were the suggested objection to be persisted in by those soi-disant reasoners who refuse to think at all about the object of this or that description, on the ground that it is “inconceivable,” I should not stop to ask them how they could say that, when that involves thinking of it in the very same breath, but should simply say that for them it would be necessary to except collections consisting of single individuals. Some of these mighty intellects refuse to allow the use of any name to denote single individuals, and also plural collections along with them; and for them the proposition ceases to be true of pairs. If they would not allow pairs to be denoted by any term that included all higher collections, the proposition would cease to be true of triplets and so on. In short, by restricting the meaning of “possible collection,” the proposition may be rendered false of small collections. No general formal restriction can render it false of greater collections.

I shall now assume that you will permit me to use the term “possible collection” according to the following definition. A “possible collection” is an ens rationis of such a nature that the definite plural of any noun, or possible noun of definite signification, (as “the A's,” “the B's,” etc.) denotes one, and only one, “possible collection” in any one perfectly definite state of the universe; and there is a certain relation between some “possible collections,” expressed by saying that one “possible collection” includes another (or the same) “possible collection,” and if, and only if, of two nouns one is universally and affirmatively predicable of the other in any one perfectly definite state of the universe, then the “possible collection” denoted by the definite plural of the former includes whatever “possible collection” is included by the “possible collection” denoted by the definite plural of the latter, and of any two different “possible collections,” one or other must include something not included by the other.

A diagram of the definition of “possible collection” being compared with a diagram embracing whatever members of subclasses 1 and 2 that it may, excluding all the rest, will now assure us that any such aggregate is a possible collection of members of the class C, no matter what individuals of Classes I and III be included or excluded in the aggregate along with those members of Class II, if any there be in the aggregate.

We shall select, then, a single possible collection of members of C to which we give the proper name, c, and this possible collection shall be one which contains no individual of Subclass 1, but contains whatever individual there may be of Subclass 2. We then ask whether or not it is true that c stands in the relation R to a member of C to which no other possible collection of members of C stands in the same relation; or, to put this question into a more convenient shape, we ask, Is there any member of the Class C to which c and no other possible collection of members of C stands in the relation R? If there be such a member or members of C, let us give one of them the proper name T. Then T must belong to one of our four divisions of this class. That is,

either T belongs to Class I (but that cannot be, since by the definition of Class I, to no member of this class is any possible collection of members of C in the relation R);

or T belongs to Subclass 1 (but that cannot be, since by the definition of that subclass, every member of it is a member of the only possible collection of members of C that is R to it, which possible collection cannot be c, because c is only known to us by a description which forbids its containing any member of Subclass 1. Now it is c, and c only, that is in the relation R to T);

or T belongs to Subclass 2 (but that cannot be, since by the definition of that subclass, no member of it is a member of the only possible collection of members of C that is R to it, which possible collection cannot be c, because the description by which alone c can be recognized makes it contain every member of Subclass 2. Now it is c only that is in the relation R to T);

or T belongs to Class III (but this cannot be, since to every member of that class, by the definition of it, more than one collection of members of C stand in the relation R, while to T only one collection, namely, c, stands in that relation).

Thus, T belongs to none of the classes of members of C, and consequently is not a member of C. Consequently, there is no such member of C; that is, no member of C to which c, and no other possible collection of members of C, stands in the relation R. But c is the proper name we were at liberty to give to whatever possible collection of members of C we pleased. Hence, there is no possible collection of members of C that stands in the relation R to a member of the class C to which no other possible collection of members of C stands in this relation R. But R is the name of any relation we please, and C is any class we please. It is, therefore, proved that no matter what class be chosen, or what relation be chosen, there will be some possible collection of members of that class (in the sense in which Nothing is such a collection) which does not stand in that relation to any member of that class to which no other such possible collection stands in the same relation.

533. When I was a boy, my logical bent caused me to take pleasure in tracing out upon a map of an imaginary labyrinth one path after another in hopes of finding my way to a central compartment. The operation we have just gone through is essentially of the same sort, and if we are to recognize the one as essentially performed by experimentation upon a diagram, so must we recognize that the other is performed. The demonstration just traced out brings home to us very strongly, also, the convenience of so constructing our diagram as to afford a clear view of the mode of connection of its parts, and of its composition at each stage of our operations upon it. Such convenience is obtained in the diagrams of algebra. In logic, however, the desirability of convenience in threading our way through complications is much less than in mathematics, while there is another desideratum which the mathematician as such does not feel. The mathematician wants to reach the conclusion, and his interest in the process is merely as a means to reach similar conclusions. The logician does not care what the result may be; his desire is to understand the nature of the process by which it is reached. The mathematician seeks the speediest and most abridged of secure methods; the logician wishes to make each smallest step of the process stand out distinctly, so that its nature may be understood. He wants his diagram to be, above all, as analytical as possible.

534. In view of this, I beg leave, Reader, as an Introduction to my defence of pragmatism, to bring before you a very simple system of diagrammatization of propositions which I term the System of Existential Graphs. For, by means of this, I shall be able almost immediately to deduce some important truths of logic, little understood hitherto, and closely connected with the truth of pragmaticism; while discussions of other points of logical doctrine, which concern pragmaticism but are not directly settled by this system, are nevertheless much facilitated by reference to it.

535. By a graph (a word overworked of late years), I, for my part, following my friends Clifford and Sylvester, the introducers of the term, understand in general a diagram composed principally of spots and of lines connecting certain of the spots. But I trust it will be pardoned to me that, when I am discussing Existential Graphs, without having the least business with other Graphs, I often omit the differentiating adjective and refer to an Existential Graph as a Graph simply. But you will ask, and I am plainly bound to say, precisely what kind of a Sign an Existential Graph, or as I abbreviate that phrase here, a Graph is. In order to answer this I must make reference to two different ways of dividing all Signs. It is no slight task, when one sets out from none too clear a notion of what a Sign is — and you will, I am sure, Reader, have noticed that my definition of a Sign is not convincingly distinct — to establish a single vividly distinct division of all Signs. The one division which I have already given has cost more labor than I should care to confess. But I certainly could not tell you what sort of a Sign an Existential Graph is, without reference to two other divisions of Signs. It is true that one of these involves none but the most superficial considerations, while the other, though a hundredfold more difficult, resting as it must for a clear comprehension of it upon the profoundest secrets of the structure of Signs, yet happens to be extremely familiar to every student of logic. But I must remember, Reader, that your conceptions may penetrate far deeper than mine; and it is to be devoutly hoped they may. Consequently, I ought to give such hints as I conveniently can, of my notions of the structure of Signs, even if they are not strictly needed to express my notions of Existential Graphs.

536. I have already noted that a Sign has an Object and an Interpretant, the latter being that which the Sign produces in the Quasi-mind that is the Interpreter by determining the latter to a feeling, to an exertion, or to a Sign, which determination is the Interpretant. But it remains to point out that there are usually two Objects, and more than two Interpretants. Namely, we have to distinguish the Immediate Object, which is the Object as the Sign itself represents it, and whose Being is thus dependent upon the Representation of it in the Sign, from the Dynamical Object, which is the Reality which by some means contrives to determine the Sign to its Representation. In regard to the Interpretant we have equally to distinguish, in the first place, the Immediate Interpretant, which is the interpretant as it is revealed in the right understanding of the Sign itself, and is ordinarily called the meaning of the sign; while in the second place, we have to take note of the Dynamical Interpretant which is the actual effect which the Sign, as a Sign, really determines. Finally there is what I provisionally term the Final Interpretant, which refers to the manner in which the Sign tends to represent itself to be related to its Object. I confess that my own conception of this third interpretant is not yet quite free from mist. Of the ten divisions of signs which have seemed to me to call for my special study, six turn on the characters of an Interpretant and three on the characters of the Object. Thus the division into Icons, Indices, and Symbols depends upon the different possible relations of a Sign to its Dynamical Object. Only one division is concerned with the nature of the Sign itself, and this I now proceed to state.

537. A common mode of estimating the amount of matter in a MS. or printed book is to count the number of words.^nP

538. A familiar logical triplet is Term, Proposition, Argument. In order to make this a division of all signs, the first two members have to be much widened. By a Seme, I shall mean anything which serves for any purpose as a substitute for an object of which it is, in some sense, a representative or Sign. The logical Term, which is a class-name, is a Seme. Thus, the term “The mortality of man” is a Seme. By a Pheme I mean a Sign which is equivalent to a grammatical sentence, whether it be Interrogative, Imperative, or Assertory. In any case, such a Sign is intended to have some sort of compulsive effect on the Interpreter of it. As the third member of the triplet, I sometimes use the word Delome (pronounce deeloam, from δήλωμα), though Argument would answer well enough. It is a Sign which has the Form of tending to act upon the Interpreter through his own self-control, representing a process of change in thoughts or signs, as if to induce this change in the Interpreter.

A Graph is a Pheme, and in my use hitherto, at least, a Proposition. An Argument is represented by a series of Graphs.

539. The Immediate Object of all knowledge and all thought is, in the last analysis, the Percept. This doctrine in no wise conflicts with Pragmaticism, which holds that the Immediate Interpretant of all thought proper is Conduct. Nothing is more indispensable to a sound epistemology than a crystal-clear discrimination between the Object and the Interpretant of knowledge; very much as nothing is more indispensable to sound notions of geography than a crystal-clear discrimination between north latitude and south latitude; and the one discrimination is not more rudimentary than the other. That we are conscious of our Percepts is a theory that seems to me to be beyond dispute; but it is not a fact of Immediate Perception. A fact of Immediate Perception is not a Percept, nor any part of a Percept; a Percept is a Seme, while a fact of Immediate Perception or rather the Perceptual Judgment of which such fact is the Immediate Interpretant, is a Pheme that is the direct Dynamical Interpretant of the Percept, and of which the Percept is the Dynamical Object, and is with some considerable difficulty (as the history of psychology shows), distinguished from the Immediate Object, though the distinction is highly significant. But not to interrupt our train of thought, let us go on to note that while the Immediate Object of a Percept is excessively vague, yet natural thought makes up for that lack (as it almost amounts to), as follows. A late Dynamical Interpretant of the whole complex of Percepts is the Seme of a Perceptual Universe that is represented in instinctive thought as determining the original Immediate Object of every Percept. Of course, I must be understood as talking not psychology, but the logic of mental operations. Subsequent Interpretants furnish new Semes of Universes resulting from various adjunctions to the Perceptual Universe. They are, however, all of them, Interpretants of Percepts.

Finally, and in particular, we get a Seme of that highest of all Universes which is regarded as the Object of every true Proposition, and which, if we name it [at] all, we call by the somewhat misleading title of “The Truth."

540. That said, let us go back and ask this question: How is it that the Percept, which is a Seme, has for its direct Dynamical Interpretant the Perceptual Judgment, which is a Pheme? For that is not the usual way with Semes, certainly. All the examples that happen to occur to me at this moment of such action of Semes are instances of Percepts, though doubtless there are others. Since not all Percepts act with equal energy in this way, the instances may be none the less instructive for being Percepts. However, Reader, I beg you will think this matter out for yourself, and then you can see — I wish I could — whether your independently formed opinion does not fall in with mine. My opinion is that a pure perceptual Icon — and many really great psychologists have evidently thought that Perception is a passing of images before the mind's eye, much as if one were walking through a picture gallery — could not have a Pheme for its direct Dynamical Interpretant. I desire, for more than one reason, to tell you why I think so, although that you should today appreciate my reasons seems to be out of the question. Still, I wish you to understand me so far as to know that, mistaken though I be, I am not so sunk in intellectual night as to be dealing lightly with philosophic Truth when I aver that weighty reasons have moved me to the adoption of my opinion; and I am also anxious that it should be understood that those reasons have not been psychological at all, but are purely logical. My reason, then, briefly stated and abridged, is that it would be illogical for a pure Icon to have a Pheme for its Interpretant, and I hold it to be impossible for thought not subject to self-control, as a Perceptual Judgment manifestly is not, to be illogical. I dare say this reason may excite your derision or disgust, or both; and if it does, I think none the worse of your intelligence. You probably opine, in the first place, that there is no meaning in saying that thought which draws no Conclusion is illogical, and that, at any rate, there is no standard by which I can judge whether such thought is logical or not; and in the second place, you probably think that, if self-control has any essential and important relation to logic, which I guess you either deny or strongly doubt, it can only be that it is that which makes thought logical, or else which establishes the distinction between the logical and the illogical, and that in any event it has to be such as it is, and would be logical, or illogical, or both, or neither, whatever course it should take. But though an Interpretant is not necessarily a Conclusion, yet a Conclusion is necessarily an Interpretant. So that if an Interpretant is not subject to the rules of Conclusions there is nothing monstrous in my thinking it is subject to some generalization of such rules. For any evolution of thought, whether it leads to a Conclusion or not, there is a certain normal course, which is to be determined by considerations not in the least psychological, and which I wish to expound in my next article; and while I entirely agree, in opposition to distinguished logicians, that normality can be no criterion for what I call rationalistic reasoning, such as alone is admissible in science, yet it is precisely the criterion of instinctive or common-sense reasoning, which, within its own field, is much more trustworthy than rationalistic reasoning. In my opinion, it is self-control which makes any other than the normal course of thought possible, just as nothing else makes any other than the normal course of action possible; and just as it is precisely that that gives room for an ought-to-be of conduct, I mean Morality, so it equally gives room for an ought-to-be of thought, which is Right Reason; and where there is no self-control, nothing but the normal is possible. If your reflections have led you to a different conclusion from mine, I can still hope that when you come to read my next article, in which I shall endeavor to show what the forms of thought are, in general and in some detail, you may yet find that I have not missed the truth.

541. But supposing that I am right, as I probably shall be in the opinions of some readers, how then is the Perceptual Judgment to be explained? In reply, I note that a Percept cannot be dismissed at will, even from memory. Much less can a person prevent himself from perceiving that which, as we say, stares him in the face. Moreover, the evidence is overwhelming that the perceiver is aware of this compulsion upon him; and if I cannot say for certain how this knowledge comes to him, it is not that I cannot conceive how it could come to him, but that, there being several ways in which this might happen, it is difficult to say which of those ways actually is followed. But that discussion belongs to psychology; and I will not enter upon it. Suffice it to say that the perceiver is aware of being compelled to perceive what he perceives. Now existence means precisely the exercise of compulsion. Consequently, whatever feature of the percept is brought into relief by some association and thus attains a logical position like that of the observational premiss of an explaining Abduction,^nP

542. That conception of Aristotle which is embodied for us in the cognate origin of the terms actuality and activity is one of the most deeply illuminating products of Greek thinking. Activity implies a generalization of effort; and effort is a two-sided idea, effort and resistance being inseparable, and therefore the idea of Actuality has also a dyadic form.

543. No cognition and no Sign is absolutely precise, not even a Percept; and indefiniteness is of two kinds, indefiniteness as to what is the Object of the Sign, and indefiniteness as to its Interpretant, or indefiniteness in Breadth and in Depth. Indefiniteness in Breadth may be either Implicit or Explicit. What this means is best conveyed in an example. The word donation is indefinite as to who makes the gift, what he gives, and to whom he gives it. But it calls no attention, itself, to this indefiniteness. The word gives refers to the same sort of fact, but its meaning is such that that meaning is felt to be incomplete unless those items are, at least formally, specified; as they are in “Somebody gives something to some person (real or artificial).” An ordinary Proposition ingeniously contrives to convey novel information through Signs whose significance depends entirely on the interpreter's familiarity with them; and this it does by means of a “Predicate,” i.e., a term explicitly indefinite in breadth, and defining its breadth by means of “Subjects,” or terms whose breadths are somewhat definite, but whose informative depth (i.e., all the depth except an essential superficies) is indefinite, while conversely the depth of the Subjects is in a measure defined by the Predicate. A Predicate is either non-relative, or a monad, that is, is explicitly indefinite in one extensive respect, as is “black"; or it is a dyadic relative, or dyad, such as “kills,” or it is a polyadic relative, such as “gives.” These things must be diagrammatized in our system.

Something more needs to be added under the same head. You will observe that under the term “Subject” I include, not only the subject nominative, but also what the grammarians call the direct and the indirect object, together, in some cases, with nouns governed by prepositions. Yet there is a sense in which we can continue to say that a Proposition has but one Subject, for example, in the proposition, “Napoleon ceded Louisiana to the United States,” we may regard as the Subject the ordered triplet, “Napoleon — Louisiana — the United States,” and as the Predicate, “has for its first member, the agent, or party of the first part, for its second member the object, and for its third member the party of the second part of one and the same act of cession.” The view that there are three subjects is, however, preferable for most purposes, in view of its being so much more analytical, as will soon appear.

544. All general, or definable, Words, whether in the sense of Types or of Tokens, are certainly Symbols. That is to say, they denote the objects that they do by virtue only of there being a habit that associates their signification with them. As to Proper Names, there might perhaps be a difference of opinion, especially if the Tokens are meant. But they should probably be regarded as Indices, since the actual connection (as we listen to talk), of Instances of the same typical words with the same Objects, alone causes them to be interpreted as denoting those Objects. Excepting, if necessary, propositions in which all the subjects are such signs as these, no proposition can be expressed without the use of Indices.^nP

545. Oh, I overhear what you are saying, O Reader: that a Universe and a Category are not at all the same thing; a Universe being a receptacle or class of Subjects, and a Category being a mode of Predication, or class of Predicates. I never said they were the same thing; but whether you describe the two correctly is a question for careful study.

546. Let us begin with the question of Universes. It is rather a question of an advisable point of view than of the truth of a doctrine. A logical universe is, no doubt, a collection of logical subjects, but not necessarily of meta-physical Subjects, or “substances"; for it may be composed of characters, of elementary facts, etc. See my definition in Baldwin's Dictionary. Let us first try whether we may not assume that there is but one kind of Subjects which are either existing things or else quite fictitious. Let it be asserted that there is some married woman who will commit suicide in case her husband fails in business. Surely that is a very different proposition from the assertion that some married woman will commit suicide if all married men fail in business. Yet if nothing is real but existing things, then, since in the former proposition nothing whatever is said as to what the lady will or will not do if her husband does not fail in business, and since of a given married couple this can only be false if the fact is contrary to the assertion, it follows it can only be false if the husband does fail in business and if the wife then fails to commit suicide. But the proposition only says that there is some married couple of which the wife is of that temper. Consequently, there are only two ways in which the proposition can be false, namely, first, by there not being any married couple, and secondly, by every married man failing in business while no married woman commits suicide. Consequently, all that is required to make the proposition true is that there should either be some married man who does not fail in business, or else some married woman who commits suicide. That is, the proposition amounts merely to asserting that there is a married woman who will commit suicide if every married man fails in business. The equivalence of these two propositions is the absurd result of admitting no reality but existence. If, however, we suppose that to say that a woman will suicide if her husband fails, means that every possible course of events would either be one in which the husband would not fail or one in which the wife would commit suicide, then, to make that false it will not be requisite for the husband actually to fail, but it will suffice that there are possible circumstances under which he would fail, while yet his wife would not commit suicide. Now you will observe that there is a great difference between the two following propositions:

First, There is some one married woman who under all possible conditions would commit suicide or else her husband would not have failed.

Second, Under all possible circumstances there is some married woman or other who would commit suicide, or else her husband would not have failed.

The former of these is what is really meant by saying that there is some married woman who would commit suicide if her husband were to fail, while the latter is what the denial of any possible circumstances except those that really take place logically leads to [our] interpreting (or virtually interpreting), the Proposition as asserting.

547. In other places, I have given many other reasons for my firm belief that there are real possibilities. I also think, however, that, in addition to actuality and possibility, a third mode of reality must be recognized in that which, as the gipsy fortune-tellers express it, is “sure to come true,” or, as we may say, is destined,^nP

548. I will proceed to explain why, although I am not prepared to deny that every proposition can be represented, and that I must say, for the most part very conveniently, under your view that the Universes are receptacles of the Subjects alone, I, nevertheless, cannot deem that mode of analyzing propositions to be satisfactory.

And to begin with, I trust you will all agree with me that no analysis, whether in logic, in chemistry, or in any other science, is satisfactory, unless it be thorough, that is, unless it separates the compound into components each entirely homogeneous in itself, and therefore free from the smallest admixture of any of the others. It follows that in the Proposition, “Some Jew is shrewd,” the Predicate is “Jew-that-is-shrewd,” and the Subject is Something, while in the proposition “Every Christian is meek,” the Predicate is “Either not Christian or else meek,” while the Subject is Anything; unless, indeed, we find reason to prefer to say that this Proposition means, “It is false to say that a person is Christian of whom it is false to say that he is meek.” In this last mode of analysis, when a Singular Subject is not in question (which case will be examined later), the only Subject is Something. Either of these two modes of analysis [differentiates] quite [clearly] the Subject from any Predicative ingredients; and at first sight, either seems quite favorable to the view that it is only the Subjects which belong to the Universes. Let us, however, consider the following two forms of propositions:

A Any adept alchemist could produce a philosopher's stone of some kind or other,

B There is one kind of philosopher's stone that any adept alchemist could produce.

We can express these in the principle that the Universes are receptacles of Subjects as follows:

A¹ The Interpreter having selected any individual he likes, and called it A, an object B can be found, such that, Either A would not be an adept alchemist, or B would be a philosopher's stone of some kind, and A could produce B.

B¹ Something, B, might be found, such that, no matter what the Interpreter might select and call A, B would be a philosopher's stone of some kind, while either A would not be an adept alchemist, or else A could produce B.

In these forms there are two Universes, the one of individuals selected at pleasure by the interpreter of the proposition, the other of suitable objects.

I will now express the same two propositions on the principle that each Universe consists, not of Subjects, but the one of True assertions, the other of False, but each to the effect that there is something of a given description.

1. This is false: That something, P, is an adept alchemist, and that this is false, that while something, S, is a philosopher's stone of some kind, P could produce S.

2. This is true: That something, S, is a philosopher's stone of some kind; and this is false, that something, P, is an adept alchemist while this is false, that P could produce S.

Here, the whole proposition is mostly made up of the truth or falsity of assertions that a thing of this or that description exists, the only conjunction being “and.” That this method is highly analytic is manifest. Now since our whole intention is to produce a method for the perfect analysis of propositions, the superiority of this method over the other for our purpose is undeniable. Moreover, in order to illustrate how that other might lead to false logic, I will tack the predicate of B1, in its objectionable form, upon the subject of A¹ in the same form, and vice versa. I shall thus obtain two propositions which that method represents as being as simple as are Nos. 1 and 2.

We shall see whether they are so. Here they are:

3. The Interpreter having designated any object to be called A, an object B may be found such that

B is a philosopher's stone of some kind, while either A is not an adept alchemist or else A could produce B.

4. Something, B, may be found, such that, no matter what the interpreter may select, and call A,

Either A would not be an adept alchemist, or B would be a philosopher's stone of some kind, and A could produce B.

Proposition 3 may be expressed in ordinary language thus: There is a kind of philosopher's stone, and if there be any adept alchemist, he could produce a philosopher's stone of some kind. That is, No. 3 differs from A, A¹ and 1 only in adding that there is a kind of philosopher's stone. It differs from B, B¹ and 2 in not saying that any two adepts could produce the same kind of stone (nor that any adept could produce any existing kind); while B, B¹ and 2 assert that some kind is both existent and could be made by every adept.

Proposition 4, in ordinary language, is: If there be (or were) an adept alchemist, there is (or would be) a kind of philosopher's stone that any adept could produce. This asserts the substance of B, B¹ and 2, but only conditionally upon the existence of an adept; but it asserts, what A, A¹ and 1 do not, that all adepts could produce some one kind of stone, and this is precisely the difference between No. 4 and A¹.

To me it seems plain that the propositions 3 and 4 are both less simple than No. 1 and less simple than No. 2, each adding some thing to one of the pair first given and asserting the other conditionally. Yet the method of treating the Universes as receptacles for the metaphysical Subjects only, involves as a consequence the representation of 3 and 4 as quite on a par with 1 and 2.

It remains to show that the other method does not carry this error with it. [If] it is the states of things affirmed or denied that are contained in the universes, then the propositions [3 and 4] become as follows:

5. This is true: that there is a philosopher's stone of some kind, S, and that it is false that there is an adept, A, and that it is false that A could produce a philosopher's stone of some kind, S'. (Where it is neither asserted nor denied that S and S' are the same, thus distinguishing this from 2.)

6. This is false: That there is an adept, A, and that this is false: That there is a stone of a kind, S, and this is false: That there is an adept, A', and that this is false: That A' could produce a stone of the kind S. (Where again it is neither asserted nor denied that A and A' are identical, but the point is that this proposition holds even if they are not identical, thus distinguishing this from 1.)

These forms exhibit the greater complexity of Propositions 3 and 4, by showing that they really relate to three individuals each; that is to say, 3 to two possible different kinds of stone, as well as to an adept; and 4 to two possible different adepts, and to a kind of stone. Indeed, the two forms 3 and 4 are absolutely identical in meaning with the following different forms on the same theory. Now it is, to say the least, a serious fault in a method of analysis that it can yield two analyses so different of one and the same compound.

7. An object, B, can be found, such that whatever object the interpreter may select and call A, an object, B', can thereupon be found such that B is an existing kind of philosopher's stone, and either A would not be an adept or else B' is a kind of philosopher's stone such as A could produce.

8. Whatever individual the Interpreter may choose to call A, an object, B, may be found, such that whatever individual the Interpreter may choose to call A', Either A is not an adept or B is an existing kind of philosopher's stone, and either A' is not an adept or else A' could produce a stone of the kind B.

But while my forms are perfectly analytic, the need of diagrams to exhibit their meaning to the eye (better than merely giving a separate line to every proposition said to be false) is painfully obtrusive.^nP

549. I will now say a few words about what you have called Categories, but for which I prefer the designation Predicaments, and which you have explained as predicates of predicates. That wonderful operation of hypostatic abstraction by which we seem to create entia rationis that are, nevertheless, sometimes real, furnishes us the means of turning predicates from being signs that we think or think through, into being subjects thought of. We thus think of the thought-sign itself, making it the object of another thought-sign. Thereupon, we can repeat the operation of hypostatic abstraction, and from these second intentions derive third intentions. Does this series proceed endlessly? I think not. What then are the characters of its different members? My thoughts on this subject are not yet harvested. I will only say that the subject concerns Logic, but that the divisions so obtained must not be confounded with the different Modes of Being: Actuality, Possibility, Destiny (or Freedom from Destiny). On the contrary, the succession of Predicates of Predicates is different in the different Modes of Being. Meantime, it will be proper that in our system of diagrammatization we should provide for the division, whenever needed, of each of our three Universes of modes of reality into Realms for the different Predicaments.

550. All the various meanings of the word “Mind,” Logical, Metaphysical, and Psychological, are apt to be confounded more or less, partly because considerable logical acumen is required to distinguish some of them, and because of the lack of any machinery to support the thought in doing so, partly because they are so many, and partly because (owing to these causes), they are all called by one word, “Mind.” In one of the narrowest and most concrete of its logical meanings, a Mind is that Seme of The Truth, whose determinations become Immediate Interpretants of all other Signs whose Dynamical Interpretants are dynamically connected. In our Diagram the same thing which represents The Truth must be regarded as in another way representing the Mind, and indeed, as being the Quasi-mind of all the Signs represented on the Diagram. For any set of Signs which are so connected that a complex of two of them can have one interpretant, must be Determinations of one Sign which is a Quasi-mind.

551. Thought is not necessarily connected with a brain. It appears in the work of bees, of crystals, and throughout the purely physical world; and one can no more deny that it is really there, than that the colors, the shapes, etc., of objects are really there. Consistently adhere to that unwarrantable denial, and you will be driven to some form of idealistic nominalism akin to Fichte's. Not only is thought in the organic world, but it develops there. But as there cannot be a General without Instances embodying it, so there cannot be thought without Signs. We must here give “Sign” a very wide sense, no doubt, but not too wide a sense to come within our definition. Admitting that connected Signs must have a Quasi-mind, it may further be declared that there can be no isolated sign. Moreover, signs require at least two Quasi-minds; a Quasi-utterer and a Quasi-interpreter; and although these two are at one (i.e., are one mind) in the sign itself, they must nevertheless be distinct. In the Sign they are, so to say, welded. Accordingly, it is not merely a fact of human Psychology, but a necessity of Logic, that every logical evolution of thought should be dialogic. You may say that all this is loose talk; and I admit that, as it stands, it has a large infusion of arbitrariness. It might be filled out with argument so as to remove the greater part of this fault; but in the first place, such an expansion would require a volume — and an uninviting one; and in the second place, what I have been saying is only to be applied to a slight determination of our system of diagrammatization, which it will only slightly affect; so that, should it be incorrect, the utmost certain effect will be a danger that our system may not represent every variety of non-human thought.

552. There now seems to remain no reason why we should not proceed forthwith to formulate and agree upon

Convention the First: Of the Agency of the Scripture. We are to imagine that two parties^nP

The two collaborating parties shall be called the Graphist and the Interpreter. The Graphist shall responsibly scribe each original Graph and each addition to it, with the proper indications of the Modality to be attached to it, the relative Quality^nP

553. Convention the Second; Of the Matter of the Scripture, and the Modality of the Phemes expressed. The matter which the Graph-instances are to determine, and which thereby becomes the Quasi-mind in which the Graphist and Interpreter are at one, being a Seme of The Truth, that is, of the widest Universe of Reality, and at the same time, a Pheme of all that is tacitly taken for granted between the Graphist and Interpreter, from the outset of their discussion, shall be a sheet, called the Phemic Sheet, upon which signs can be scribed and from which any that are already scribed in any manner (even though they be incised) can be erased. But certain parts of other sheets not having the significance of the Phemic sheet, but on which Graphs can be scribed and erased, shall be sometimes inserted in the Phemic sheet and exposed to view, as the Third Convention shall show. Every part of the exposed surface shall be tinctured in one or another of twelve tinctures.

THE TINCTURES

Fig. 197

554. When any representation of a state of things consisting in the applicability of a given description to an individual or limited set of individuals otherwise indesignate is scribed, the Mode of Tincture of the province on which it is scribed shows whether the Mode of Being which is to be affirmatively or negatively attributed to the state of things described is to be that of Possibility, when Color will be used; or that of Intention, indicated by Fur; or that of Actuality shown by Metal. Special understandings may determine special tinctures to refer to special varieties of the three genera of Modality. Finally, the Mode of Tincture of the March may determine whether the Entire Graph is to be understood as Interrogative, Imperative, or Indicative.

555. Convention the Third: Of Areas enclosed within, but severed from, the Phemic Sheet. The Phemic Sheet is to be imagined as lying on the smoother of the two surfaces or sides of a Leaf, this side being called the recto, and to consist of so much of this side as is continuous with the March. Other parts of the recto may be exposed to view. Every Graph-instance on the Phemic Sheet is posited unconditionally (unless, according to an agreement between Graphist and Interpreter, the Tincture of its own Province or of the March should indicate a condition) and every Graph-instance on the recto is posited affirmatively and, in so far as it is indeterminate, indefinitely.

556. Should the Graphist desire to negative a Graph, he must scribe it on the verso, and then, before delivery to the Interpreter, must make an incision, called a Cut, through the Sheet all the way round the Graph-instance to be denied, and must then turn over the excised piece, so as to expose its rougher surface carrying the negatived Graph-instance. This reversal of the piece is to be conceived to be an inseparable part of the operation of making a Cut.^nP

557. There may be any number of Cuts, one within another, the Area of one being the Place of the next, and since the Area of each is on the side of the leaf opposite to its Place, it follows that recto Areas may be exposed which are not parts of the Phemic Sheet. Every Graph-instance on a recto Area is affirmatively posited, but is posited conditionally upon whatever may be signified by the Graph on the Place of the Cut of which this Area is the Area. (It follows that Graphs on Areas of different Enclosures on a verso Place are only alternately affirmed, and that while only the Entire Graph of the Area of an Enclosure on a recto Place is denied, but not its different Partial Graphs, except alternatively, the Entire Graphs of Areas of different Enclosures on one recto Place are copulatively denied.)

558. Every Graph-instance must lie upon one Area,^nP

559. Convention the Fourth: Concerning Signs of Individuals and of Individual Identity. A single dot, not too minute, or single congeries of contiguous pretty large dots, whether in the form of a line or surface, when placed on any exposed Area, will refer to a single member of the Universe to which the Tincture of that Area refers, but will not thereby be made to refer determinately to any one. But do not forget that separate dots, or separate aggregates of dots, will not necessarily denote different Objects.

560. By a rheme, or predicate, will here be meant a blank form of proposition which might have resulted by striking out certain parts of a proposition, and leaving a blank in the place of each, the parts stricken out being such that if each blank were filled with a proper name, a proposition (however nonsensical) would thereby be recomposed. An ordinary predicate of which no analysis is intended to be represented will usually be written in abbreviated form, but having a particular point on the periphery of the written form appropriated to each of the blanks that might be filled with a proper name. Such written form with the appropriated points shall be termed a Spot; and each appropriated point of its periphery shall be called a Peg of the Spot. If a heavy dot is placed at each Peg, the Spot will become a Graph expressing a proposition in which every blank is filled by a word (or concept) denoting an indefinite individual object, “something.”

561. A heavy line shall be considered as a continuum of contiguous dots; and since contiguous dots denote a single individual, such a line without any point of branching will signify the identity of the individuals denoted by its extremities, and the type of such unbranching line shall be the Graph of Identity, any instance of which (on one area, as every Graph-instance must be) shall be called a Line of Identity. The type of a three-way point of such a line (Fig. 198) shall be the Graph of Teridentity; and it shall be considered as composed of three contiguous Pegs of a Spot of Identity.

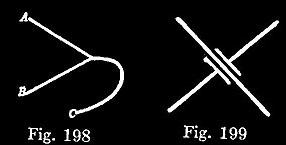
In order to avoid the intersection of Lines of Identity, either a Selective may be employed, or a Bridge, which is imagined to be a bit of paper ribbon, but will in practice be pictured as in Fig. 199.

562. Convention the Fifth: Of the Connections of Graph-Instances. Two partial Graph-Instances are said to be individually and directly connected, if, and only if, in the Entire Graph, one individual is, either unconditionally or under some condition, and whether affirmatively or negatively, made a Subject of both. Two Graph-Instances connected by a ligature are explicitly and definitely individually and directly connected. Two Graph-Instances in the same Province are thereby explicitly, although indefinitely, individually and directly connected, since both, or one and the negative of the other, or the negative of both, are asserted to be true or false together, that is, under the same circumstances, although these circumstances are not formally defined, but are left to be interpreted according to the nature of the case. Two Graph-Instances not in the same Province, though on the same Mode of Tincture, are only in so far connected that both are in the same Universe. Two Graph-Instances in different Modes of Tincture are only in so far connected that both, or one and the negative of the other, or the negative of both, are posited as appertaining to the Truth. They cannot be said to have any individual and direct connection. Two Graph-Instances that are not individually connected within the innermost Cut which contains them both cannot be so connected at all; and every ligature connecting them is meaningless and may be made or broken.

563. Relations which do not imply the occurrence in their several universes of all their correlates must not be expressed by Spots or single Graphs,^nP

564. I will now proceed to give a few examples of Existential Graphs in order to illustrate the method of interpretation, and also the Permissions of Illative Transformation of them.

If you carefully examine the above conventions, you will find that they are simply the development, and excepting in their insignificant details, the inevitable result of the development of the one convention that if any Graph, A, asserts one state of things to be real and if another graph, B, asserts the same of another state of things, then AB, which results from setting both A and B upon the sheet, shall assert that both states of things are real. This was not the case with my first system of Graphs, described in Vol. VII of The Monist, which I now call Entitative Graphs. But I was forced to this principle by a series of considerations which ultimately arrayed themselves into an exact logical deduction of all the features of Existential Graphs which do not involve the Tinctures. I have no room for this here; but I state some of the points arrived at somewhat in the order in which they first presented themselves.

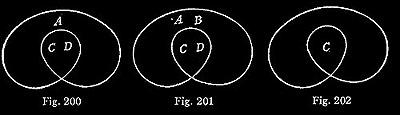
In the first place, the most perfectly analytical system of representing propositions must enable us to separate illative transformations into indecomposable parts. Hence, an illative transformation from any proposition, A, to any other, B, must in such a system consist in first transforming A into AB, followed by the transformation of AB into B. For an omission and an insertion appear to be indecomposable transformations and the only indecomposable transformations. That is, if A can be transformed by insertion into AB, and AB by omission in[to] B, the transformation of A into B can be decomposed into an insertion and an omission. Accordingly, since logic has primarily in view argument, and since the conclusiveness of an argument can never be weakened by adding to the premisses nor by subtracting from the conclusion, I thought I ought to take the general form of argument as the basal form of composition of signs in my diagrammatization; and this necessarily took the form of a “scroll,” that is (see Figs. 200, 201, 202) a curved line without contrary flexure and returning into itself after once crossing itself, and thus forming an outer and an inner “close.”

Fig. 203	Fig. 204

565. The first permission of illative transformation is now evident as follows:

First Permission, called “The Rule of Deletion and Insertion.” Any Graph-Instance can be deleted from any recto Area (including the severing of any Line of Identity), and any Graph-Instance can be inserted on any verso Area (including as a Graph-Instance the juncture of any two Lines of Identity or Points of Teridentity).

566. The justice of the following will be seen instantly by students of any form of Logical Algebra, and with very little difficulty by others:

Second Permission, called “The Rule of Iteration and Deiteration.” Any Graph scribed on any Area may be Iterated in or (if already Iterated) may be Deiterated by a deletion from that Area or from any other Area included within that. This involves the Permission to distort a line of Identity, at will.

To iterate a Graph means to scribe it again, while joining by Ligatures every Peg of the new Instance to the corresponding Peg of the Original Instance. To deiterate a Graph is to erase a second Instance of it, of which each Peg is joined by a Ligature to a first Instance of it. One Area is said to be included within another if, and only if, it either is that Area or else is the Area of a Cut whose Place is an Area which, according to this definition, must be regarded as included within that other. By this Permission, Fig. 205 may be transformed into Fig. 206, and thence, by Permission No. 1, into Fig. 207.

Fig. 205	Fig. 206	Fig. 207

567. We now come to the Third Permission, which I shall state in a form which is valid, sufficient for its purpose, and convenient in practice, but which cannot be assumed as an undeduced Permission, for the reason that it allows us to regard the Inner close, after the Scroll is removed, as being a part of the Area on which the Scroll lies. Now this is not strictly either an Insertion or a Deletion; and a perfectly analytical System of Permissions should permit only the indecomposable operations of Insertion and Deletion of Graphs that are simple in expression. The more scientific way would be to substitute for the Second and Third Permissions the following Permission:

If an Area, Υ, and an Area, Ω , be related in any of these four ways, viz., (1) If Υ and Ω are the same Area; (2) If Ω is the Area of an Enclosure whose Place is Υ; (3) if Ω is the Area of an Enclosure whose Place is the Area of a second Enclosure whose Place is Υ; or (4) if Ω is the Place of an Enclosure whose Area is vacant except that it is the Place of an Enclosure whose Area is Υ, and except that it may contain ligatures, identifying Pegs in Ω with Pegs in Υ; then, if Ω be a recto area, any simple Graph already scribed upon Υ may be iterated upon Ω ; while if Ω be a verso Area, any simple Graph already scribed upon Υ and iterated upon Ω may be deiterated by being deleted or abolished from Ω .

These two Rules (of Deletion and Insertion, and of Iteration and Deiteration) are substantially all the undeduced Permissions needed; the others being either Consequences or Explanations of these. Only, in order that this may be true, it is necessary to assume that all indemonstrable implications of the Blank have from the beginning been scribed upon distant parts of the Phemic Sheet, upon any part of which they may, therefore, be iterated at will. I will give no list of these implications, since it could serve no other purpose than that of warning beginners that necessary propositions not included therein were deducible from the other permissions. I will simply notice two principles the neglect of which might lead to difficulties. One of these is that it is physically impossible to delete or otherwise get rid of a Blank in any Area that contains a Blank, whether alone or along with other Graph-Instances. We may, however, assume that there is one Graph, and only one, an Instance of which entirely fills up an Area, without any Blank. The other principle is that, since a Dot merely asserts that some individual object exists, and is thus one of the implications of the Blank, it may be inserted in any Area; and since the Dot will signify the same thing whatever its size, it may be regarded as an Enclosure whose Area is filled with an Instance of that sole Graph that excludes the Blank. The Dot, then, denies that Graph, which may, therefore, be understood as the absurd Graph, and its signification may be formulated as “Whatever you please is true.” The absurd Graph may also take the form of an Enclosure with its Area entirely Blank, or enclosing only some Instance of a Graph implied in the Blank. These two principles will enable the Graphist to thread his way through some Transformations which might otherwise appear paradoxical and absurd.

Third Permission, called “The Rule of the Double Cut.” Two Cuts one within another, with nothing between them, unless it be Ligatures passing from outside the outer Cut to inside the inner one, may be made or abolished on any Area.

568. Let us now consider the Interpretation of such Ligatures. For that purpose, I first note that the Entire Graph of any recto Area is a wholly particular and affirmative Proposition or Copulation of such Propositions. By “wholly particular,” I mean, having for every Subject an indesignate individual. The Entire Graph of any verso Area is a wholly universal negative proposition or a disjunction of such propositions.

The first time one hears a Proper Name pronounced, it is but a name, predicated, as one usually gathers, of an existent, or at least historically existent, individual object, of which, or of whom, one almost always gathers some additional information. The next time one hears the name, it is by so much the more definite; and almost every time one hears the name, one gains in familiarity with the object. A Selective is a Proper Name met with by the Interpreter for the first time. But it always occurs twice, and usually on different areas. Now the Interpretation, by Convention No. 3, is to be Endoporeutic, so that it is the outermost occurrence of the Name that is the earliest.

Fig. 208

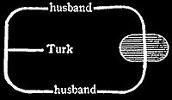
569. Let us now analyze the interpretation of a Ligature passing through a Cut. Take, for example, the Graph of Fig. 208. The partial Graph on the Place of the Cut asserts that there exists an individual denoted by the extremity of the line of identity on the Cut, which is a millionaire. Call that individual C. Then, since contiguous dots denote the same individual objects, the extremity of the line of identity on the Area of the cut is also C, and the Partial Graph on that Area, asserts that, let the Interpreter choose whatever individual he will, that individual is either not C, or else is not unfortunate. Thus, the Entire Graph asserts that there exists a millionaire who is not unfortunate. Furthermore, the Enclosure lying in the same Argent Province as the “millionaire,” it is asserted that this individual's being a millionaire is connected with his not being unfortunate. This example shows that the Graphist is permitted to extend any Line of Identity on a recto Area so as to carry an end of it to any Cut in that area. Let us next interpret Fig. 209.

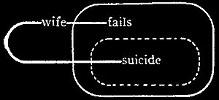
Fourth Permission. If the smallest Cut which wholly contains a Ligature connecting two Graphs in different Provinces has its Area on the side of the Leaf opposite to that of the Area of the smallest Cut that contains those two Graphs, then such Ligature may be made or broken at pleasure, as far as these two Graphs are concerned.

570. Another somewhat curious problem concerning ligatures is to say by what principle it is true, as it evidently is true, that the passage of ligatures from without the outer of two Cuts to within the inner of them will not prevent the two from collapsing in case there is no other Graph-Instance between them. A little study suffices to show that this may depend upon the ligatures' being replaceable by Selectives where they cross the Cuts, and that a Selective is always, at its first occurrence, a new predicate. For it is a principle of Logic that in introducing a new predicate one has a right to assert what one likes concerning it, without any restriction, as long as one implies no assertion concerning anything else. I will leave it to you, Reader, to find out how this principle accounts for the collapse of the two Cuts. Another solution of this problem, not depending on the superfluous device of Selectives, is afforded by the second enunciation of the Rule of Iteration and Deiteration; since this permits the Graph of the Inner Close to be at once iterated on the Phemic Sheet. One may choose between these two methods of solution.

571. The System of Existential Graphs which I have now sufficiently described — or, at any rate, have described as well as I know how, leaving the further perfection of it to others — greatly facilitates the solution of problems of Logic, as will be seen in the sequel, not by any mysterious properties, but simply by substituting for the symbols in which such problems present themselves, concrete visual figures concerning which we have merely to say whether or not they admit certain describable relations of their parts. Diagrammatic reasoning is the only really fertile reasoning. If logicians would only embrace this method, we should no longer see attempts to base their science on the fragile foundations of metaphysics or a psychology not based on logical theory; and there would soon be such an advance in logic that every science would feel the benefit of it.

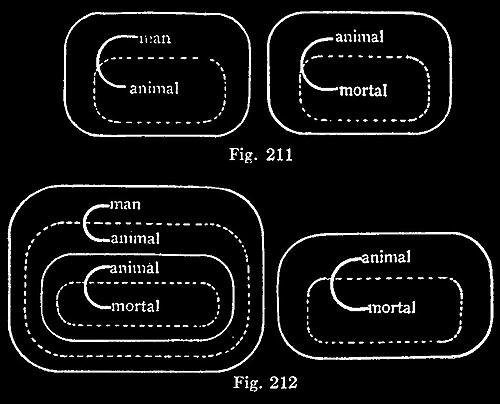
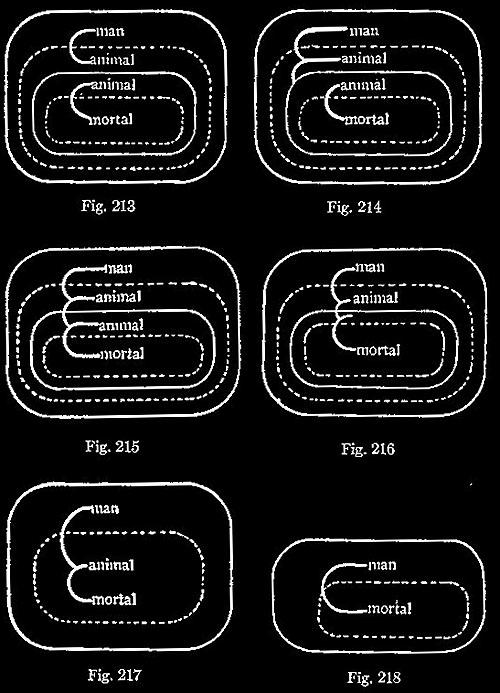
This System may, of course, be applied to the analysis of reasonings. Thus, to separate the syllogistic illation, “Any man would be an animal, and any animal would be mortal; therefore, any man would be mortal,” the Premisses are first scribed as in Fig. 211. Then by the rule of Iteration, a first illative transformation gives Fig. 212. Next, by the permission to erase from a recto Area, a second step gives Fig. 213. Then, by the permission to deform a line of Identity on a recto Area, a third step gives Fig. 214. Next, by the permission to insert in a verso Area, a fourth step gives Fig. 215. Next, by Deiteration, a fifth step gives Fig. 216.

572. I mentioned on an early page of this paper that this System leads to a different conception of the Proposition and Argument from the traditional view that a Proposition is composed of Names, and that an Argument is composed of Propositions. It is a matter of insignificant detail whether the term Argument be taken in the sense of the Middle Term, in that of the Copulate of Premisses, in that of the setting forth of Premisses and Conclusion, or in that of the representation that the real facts which the premisses assert (together, it may be, with the mode in which those facts have come to light) logically signify the truth of the Conclusion. In any case, when an Argument is brought before us, there is brought to our notice (what appears so clearly in the Illative Transformations of Graphs) a process whereby the Premisses bring forth the Conclusion, not informing the Interpreter of its Truth, but appealing to him to assent thereto. This Process of Transformation, which is evidently the kernel of the matter, is no more built out of Propositions than a motion is built out of positions. The logical relation of the Conclusion to the Premisses might be asserted; but that would not be an Argument, which is essentially intended to be understood as representing what it represents only in virtue of the logical habit which would bring any logical Interpreter to assent to it. We may express this by saying that the Final (or quasi-intended) Interpretant of an Argument represents it as representing its Object after the manner of a Symbol. In an analogous way the relation of Predicate to Subject which is stated in a Proposition might be merely described in a Term. But the essence of the Proposition is that it intends, as it were, to be regarded as in an existential relation to its Object, as an Index is, so that its assertion shall be regarded as evidence of the fact. It appears to me that an assertion and a command do not differ essentially in the nature of their Final Interpretants as in their Immediate, and so far as they are effective, in their Dynamical Interpretants; but that is of secondary interest. The Name, or any Seme, is merely a substitute for its Object in one or another capacity in which respect it is all one with the Object. Its Final Interpretant thus represents it as representing its Object after the manner of an Icon, by mere agreement in idea. It thus appears that the difference between the Term, the Proposition, and the Argument, is by no means a difference of complexity, and does not so much consist in structure as in the services they are severally intended to perform.

For that reason, the ways in which Terms and Arguments can be compounded cannot differ greatly from the ways in which Propositions can be compounded. A mystery, or paradox, has always overhung the question of the Composition of Concepts. Namely, if two concepts, A and B, are to be compounded, their composition would seem to be necessarily a third ingredient, Concept C, and the same difficulty will arise as to the Composition of A and C. But the Method of Existential Graphs solves this riddle instantly by showing that, as far as propositions go, and it must evidently be the same with Terms and Arguments, there is but one general way in which their Composition can possibly take place; namely, each component must be indeterminate in some respect or another; and in their composition each determines the other. On the recto this is obvious: “Some man is rich” is composed of “Something is a man” and “something is rich,” and the two somethings merely explain each other's vagueness in a measure. Two simultaneous independent assertions are still connected in the same manner; for each is in itself vague as to the Universe or the “Province” in which its truth lies, and the two somewhat define each other in this respect. The composition of a Conditional Proposition is to be explained in the same way. The Antecedent is a Sign which is Indefinite as to its Interpretant; the Consequent is a Sign which is Indefinite as to its Object. They supply each the other's lack. Of course, the explanation of the structure of the Conditional gives the explanation of negation; for the negative is simply that from whose Truth it would be true to say that anything you please would follow de inesse.

In my next paper, the utility of this diagrammatization of thought in the discussion of the truth of Pragmaticism shall be made to appear.