| Lowell 1 | Peirce MS 467 (SPIN) | Arisbe | Peirce pages on this site |
This unfinished manuscript was clearly intended to be the beginning of one of the Lowell Lectures, but which one is not clear. It may not have been used at all in the actual lecture series. It was previously published in NEM v.3, pp. 355-64.
Robin Catalogue: 466. Useful for 3rd or 4th?
A. MS., notebook, n.p., 1903, pp. 1-28, unfinished, with two p. 19's, both of which leave text intact.
Mathematics and logic; existential graphs introduced initially to illuminate the nature of pure mathematics, and then used in the discussion of multitude.
Ladies and Gentlemen:
Mathematics is the science which draws necessary conclusions. Such was the definition given first by my father as early as 1870. At that day, when the new mathematics was in its infancy, the novelty of this definition was disconcerting even to the profoundest mathematicians; but today nobody would propose a definition differing much from that. The only doubt that should entertain is whether we ought not to recognize as a part of mathematics, what is certainly a most important part of the mathematician's business, the formation of the assumptions on which his reasoning is to be based.
Some of the mathematicians who have the most deeply studied the fundamentals of their science have even gone so far as to pronounce mathematics to be a branch of logic. Dedekind is one of these whose two little books published in one volume in translation by the Open Court Company, which is doing so much for American culture, I should strongly recommend to your attention. The fact that so profound a mathematician can hold this opinion is a sufficient justification of my devoting several lectures of this short course to a study of the nature of mathematics.
I do not quite agree with Dedekind, myself; and I will tell you why presently. The question of whether mathematics was a branch of logic was the subject of careful discussion between my father and me at the time be had his definition under consideration. But first I had better notice an objection which will seem weighty to superficial minds. Namely, it will be said that much necessary reasoning is not at all mathematical. On that I take direct issue. Eminent jurists, moralists, and philosophers can be found whose powers of reasoning are famous, and who yet declare that they have no head for mathematics. This is, in part, a delusion owing to bad instruction which has given rise to such an aversion to everything that seems mathematical that as soon as one talks to them of x, y, z, they stop thinking. But what is also true of those persons is that they cannot hold clearly before their minds intricate relations between objects that are almost exactly alike except in respect to abstract relations. But when I ask one of those gentlemen to give me an example of a necessary reasoning that he considers not to be mathematical, it turns out to be one of those that are most readily amenable to mathematical representation, differing only from the reasoning he cannot grasp in its extreme simplicity. But that which conclusively stamps all necessary reasoning as mathematical is that in such reasoning, it makes not the slightest difference whether the premisses express observed facts (as strictly speaking they seldom do) or whether they describe wholly imaginary states of things. The conclusion follows as necessarily concerning the imaginary state of things as it would if that state of things had been observed. This, indeed, is precisely what the necessity of such reasoning consists in. For the purposes of the reasoning, therefore, the premisses are mere assumptions. If they happen to be more, it has nothing to do with the reasoning. Now the only science which deals with pure assumptions regardless of their real truth is mathematics. That is, on the whole, the best definition of mathematics. All necessary reasonings, therefore, are pieces of mathematics.
The only reason I do not agree with Dedekind in making mathematics a branch of logic is that logic is not a science of pure assumptions but is a study of positive truth. The mathematician seeks only to trace out the consequences of his assumptions in the readiest and speediest way. The logician does not care much what the conclusions from this or that system of assumptions may be. What he is interested in is in dissecting reasonings, in finding out what their elementary steps are, and in showing what positive facts about the real universe of things and of thoughts it is from which the necessity of the mathematician's reasonings and the validity of other kinds of reasonings depend, and exactly what the nature of that dependence is. I have already pointed out that the characters that make a system of symbols good for [mathematical] purposes are quite contrary to those which would make it good for logical purposes. The truth is that the mathematician and the logician meet in one department on a common highway. They meet; but one is facing one way while the other is facing just the other way. Each of them, it is true, finds it interesting to turn round occasionally and take a glance in the opposite direction.
The mathematician, however, has little or nothing to learn of the logician. Mathematics differs from all the special sciences whether of physics or of psychics in never encountering logical difficulties, which it does not lie entirely within his own competence to resolve. The logician on the other hand has everything to learn from the mathematician. Mathematics is, with the exception of Phenomenology and Ethics, the only science from which he can draw any real guidance. There is therefore every reason in the world why we should not delay examining the fundamental nature of mathematics.
The simplest possible kind of mathematics would be the mathematics of a system of only two values. Do we in experience meet with any case in which such mathematics could have any application? I reply that we do. There are just two values that any assertion can have. It is either true when it has all the value it can have, or it is false, and has no value at all. It follows that our system of Existential Graphs is precisely an application of the mathematics of two values. It will give you an idea of what Pure Mathematics is to imagine the Existential Graphs to be described without any allusion whatever to their interpretation, but to be defined as symbols subject to the fundamental rules of transformation. Namely,
1st, Graphs are figures drawn on a surface and composed of any finite number including zero of each of these 3 kinds of elements: 1st oval cuts of which no two intersect, 2nd heavy lines, and 3rd spots each with definite places each of which is at an extremity of a heavy line.
2nd, Any graph within an even number of cuts can be erased and any within an odd number of existing cuts can be inserted.
3rd, Any graph can be iterated or deiterated provided the iterated or deiterated replica is not outside of any cut that the other is inside of.
4th, Two cuts one inside the other with nothing between except heavy lines passing from within the inner to outside the outer, can either be made or destroyed anywhere.
5th, A heavy line of which both ends connect with lines inside a cut which lines do not connect spots connected inside the cut can anywhere be erased or inserted.
From those assumptions everything universally true of existential graphs could be deduced, and that would be the Pure Mathematical Treatment. I have defined Mathematics in general as the science which draws necessary conclusions and which formulates the assumptions from which such conclusions can be drawn. I now define Pure Mathematics as that Mathematics which leaves its assumptions entirely indeterminate in respects which have no bearing upon the manner in which they can be combined to produce conclusions.
The Pure Mathematics of the System of Two Values would leave us free to regard the Graphs as representing anything for which their fundamental transformations would hold good.
In like manner there would be a Mathematics of a System of Three Values which would not be without utility and which has been in some measure developed. The theory of numbers furnishes partial developments of the mathematics of every system having a finite multitude of values.
I particularly call your attention to my use of the word Multitude. I never use this word to mean a Collection or Plural. I always use it as an abstract noun denoting that character of a Collection which makes it greater than some collections and less than others. Thus, twoness, tenness, three-hundred-and-sixty-five-ness, are individual Multitudes, as I use the word.
At the very outset of the study of the logic of mathematics our attention is forced to the subject of Multitude. Everybody knows that there is a Mathematics of Multitude; and I am going this evening to tell you some elementary things about it that you probably do not know.
It is desirable to remark at the outset that the Mathematics of Multitude is not pure mathematics. The reason is that the whole
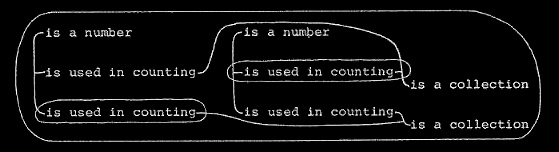
The third proposition is that there is a number next greater than any given number or taking any number whatever, there is a number (namely, the next greater one) such that taking any number you please either this third number (being no greater than the first) is used in counting every collection that the first is used in counting or else (being as great as the next greater number) is not used in counting any collection unless that next greater is used in counting it.
By manipulating those four graphs according to the rules of graphs we could reach every theorem of the mathematics of whole numbers. But the rules of the transformation of graphs do not depend upon what is written in the different spots. So long as they are preserved the same or different, as the case may be, letters or any other meaningless expressions might be substituted. In particular, in place of “collections” any other universe might be adopted, and in place of “is used in counting” a general symbol for any one dyadic relation. If this change were made in the four graphs, the result would be that they would define the relations of ordinal numbers to one another, except of course that they omit to say that there is a smallest number; and in fact there is not, if negative numbers are included.
Thus, the Arithmetic of Ordinal Numbers is Pure Mathematics; but the Arithmetic of Cardinal Numbers is Applied Mathematics. The conception of a Collection is, therefore, not a mathematical conception and the conception of Multitude is not a purely mathematical conception. But the conception of a collection is a highly important logical conception and for that reason, we will turn our attention to Multitude.
But why should the conception of Multitude be an important conception in logic? I will tell you. We have seen that there are three relations which subsist between the parts of graphs. The first is the relation expressed by the scroll 
. This is the most important of all, since this is the relation of premiss and conclusion; that is, if it be true that if A is true B is true, then should A occur as a premiss we have a right to conclude B. The second relation is that expressed by writing two graphs side by side AB, that is to say, the relation of coexistence, and the third is the relation of individual identity expressed by the heavy line. Now whatever relation is analogous to one of these three relations will be expressed by graphs into which the corresponding element of graphs enters and will therefore affect reasoning and hence will be of logical importance. Now the relation expressed by saying that one collection is at least as great as another is precisely analogous to the relation expressed by the scroll in graphs; and that is why multitude, which is the character of a collection which constitutes it as great as what it is as great as, is so very important for logic.
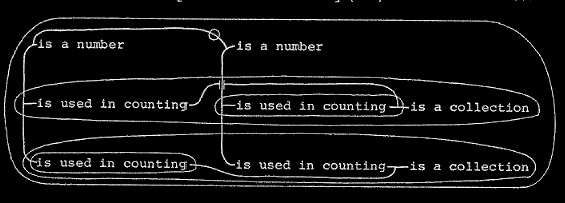
Everything depends, in logic, upon formulating precise definitions. Now what precisely do we mean by saying that one collection is at least as small as another. The best definitions are those which express how the truth or falsity of the term defined will affect what we can do in the future. To say that a thing is soft is to say that it can easily be scratched. To say that is is hard is to say that it never will easily be scratched, unless it turns soft. The relation of greater and less was first defined in this fashion by the Catholic logician Bolzano in his posthumous work which appeared in 1851. He said a collection, say that of the As is at least as small as another collection, say that of the Bs, if, and only if, every single A can be placed in a relation to B to which no other A stands in the same relation. But just as to say that a body can easily be scratched is the same as to say that it is soft, so to say that one thing can be placed in relation to another thing is to say that it already is in relation to that thing; and it is simpler to say that the collection of the As is at least as small as the collection of the Bs, if and only if there is a relation in which every A stands to a B to which no other A stands in the same relation.There is a certain dyadic relation such that if there is an A it stands in that relation to a B and if there is any A and it stands in that same relation to that same B then it is identical with that first A.
Hence we get the proposition if the collection of As is not as small as the collection of Bs then the collection of Bs must be as small as the collection of As.
This proposition has been a great puzzle to the mathematicians. They have endeavored in vain to prove it. The truth is that it never can be mathematically proved because it depends upon the peculiar nature of relations which is a question of logic, not of mathematics. Hence, every proposed mathematical demonstration of it, of which there have been more than one, will necessarily be found upon examination to be fallacious.
Whatever things we may take it into our heads to regard as forming a collection,— say the milky way, this bit of chalk, and King Peter of Servia,— have some character in common not possessed by anything else in the universe. For it is a fact that they might be regarded as forming a collection which should exclude everything else; and just as the fact that a piece of chalk could easily be scratched constitutes it eternally true that it is soft now, so the fact that any things could be regarded as forming a collection containing nothing else constitutes a character which they all possess and they alone. Qualities or characters, like relations, are in themselves mere possibilities. Many possible things do not exist but whatever at any time exists or is even imagined to exist is possible. You must try to understand, what I know is difficult to understand without long explanations for which I have no time, that I do not at any time in this course touch upon metaphysics and that here at least I have nothing to do with epistemology. I must be understood in a purely logical sense, when I say that qualities and relations are not creatures of the mind, but are in themselves eternal possibilities, whether the mind thinks them to be so or not. They acquire existence only in the sense that they determine existent individual subjects. One of you may say to another “For all the lecturer says, I think qualities are creations of the mind.” In saying that, you mean one or other of two things. You are either speaking as a metaphysician or as an epistemologist. I neither affirm nor deny what you say. I am simply talking logic. You are thinking either of the nature of the being of qualities or of the processes of human cognition. I have nothing to do with either. I simply say that in order to avoid getting wound up in your reasoning, you are to regard qualities in a certain aspect. You need not say what they really are nor what the genesis of the ideas is, but leaving that quite aside you are to regard qualities as eternal and immutable possibilities prior to existence in the sense that no fact of existence can affect in the least the qualities themselves. A collection is also a possibility, a mere possibility. But it differs from a quality in that it is a possibility posterior to existence. [::·] Here are five dots, and the existence of those five dots constitutes the existence of the collection. I might put in a sixth dot, and the possibility of that sixth constitutes the possibility of a collection of six dots. The existence of those five dots not only constitutes the existence of the one collection of five dots but also the existence of five collections of 4 dots each, as well as 10 collections of 3 dots each, 10 collections of 2 dots each, 5 collections of 1 dot each, and 1 collection nothing; and these 32 collections constitute one collection of collections. Or we may say there is a collection of six collections each of which latter collections is a collection of equal collections of dots. The members of every collection possess some quality common to them and possessed by nothing else in the universe; and for that reason it is for some purposes much the same thing to say that an object belongs to a collection and to say that it possesses a quality. But for other purposes the distinction is important. Qualities possess no individual identity but only similarity while a collection is a single individual collection, though possessing it is true only a derived individuality.
A quality possesses, in itself, few positive qualities, which few are mostly of the particular kind called quantities. Thus, any particular kind of red, has its degree of light, its degree of fullness of color, and its peculiar quality of hue. This third is something more than a mere quantity. But it varies only in two opposite ways like a quantity. A collection, on the other hand, bas all sorts of qualities discoverable by experience. Thus, a man's body is a collection of molecules; and its qualities are what is true of some of these molecules in relation to each other and to other things. Multitude is a quality of a collection or something like that; and accordingly it possesses only one quality which is its quantity. It consists in the collection's being more than some and less than others. But I do not know
Robin: 467. C. S. Peirce's Lowell Lectures for 1903. Lecture 4. A. MS., 2 notebooks, G-1903-2a, pp. 1-96. Two volumes comprise the fourth lecture, with the first volume entitled “Gamma Part of Existential Graphs.” Volumes I and II (pp. 1-96) published as 4.510-529, with deletions. Deleted: brief history of exact logic, i.e., logic begun by De Morgan, including CSP's entitative and existential graphs (pp. 8-18). Opium's dormitive virtue; abstraction, including Hegel's abuse of the term (pp. 66-78).
Paragraph numbers from CP 4 are given here for convenience of reference, but the text is that of MS 467, including parts deleted in CP 4.
Ladies and Gentlemen:
510. The alpha part of graphs, of which I gave you a tolerably full account, although without illustrating the use of it, since there was no time for that, is able to represent no reasonings except those which turn upon the logical relations of general terms.
511. The beta part, of which I was able to give you nothing more than a few scraps, has been thoroughly elaborated. It is able to handle with facility and dispatch reasonings of a very intricate kind, and propositions which ordinary language can only express by means of long and confusing circumlocutions. A person who has learned to think in beta graphs has ideas of the utmost clearness and precision which it is practically impossible to communicate to the mind of a person who has not that advantage. Its reasonings generally turn upon the properties of the relations of individual objects to one another.
But it is able to do nothing at all with many ideas which we are all perfectly familiar with. Generally speaking it is unable to reason about abstractions. It cannot reason for example about qualities nor about relations as subjects to be reasoned about. It cannot reason about ideas. It is to supply that defect that the gamma part of the subject has been invented. But this gamma part is still in its infancy. It will be many years before my successors will be able to bring it to the perfection to which the alpha and beta parts have been brought. For logical investigation is very slow, involving as it does the taking up of a confused mass of ordinary ideas, embracing we know not what and going through with a great quantity of analyses and generalizations and experiments before one can so much as get a new branch fairly inaugurated.
Exact logic was started by Augustus De Morgan in 1846, who produced a great variety of necessary reasonings entirely beyond the scope of the traditional logic, and in particular made a considerable investigation of the logic of relations, of syllogisms of transposed quantity, and of numerically definite syllogisms.
In 1847, George Boole, a great genius, produced an algebra of logic which was equivalent to the alpha part of existential graphs; but he subsequently used it to take important steps toward correcting the doctrine of probabilities.
De Morgan had many pupils, and among them Jevons who did some good work. I took up the subject about 1860, and lectured at this Institution upon it in 1866. I published various papers relating to the beta part of the subject, always employing some modification of the Algebra of Boole which I brought to perfection in Note B appended to the Johns Hopkins Studies in Logic.
Meantime Schröder, beginning in 1877, had been working up the details of the matter. Schröder's work was almost entirely in details. In the fundamentals he was less strong.
The Johns Hopkins studies, however, contained an essay of extraordinary power, fairly rivalling that of De Morgan, if not Boole's, by Dr. Oscar Howard Mitchell. In consequence of the study of that paper, in 1885 I first broke ground in the gamma part of the subject.
In 1895 Schröder published the third huge volume of his logic, which consisted mainly of a vast elaboration in detail of the logical algebra of my Note B. That I never considered that algebra to be a great masterpiece is sufficiently shown by my giving my exposition of it no other title than “Note B.” The perusal of Schröder's book convinced me that the algebra was not what was wanted; and in the Monist for January 1897 I produced a system of graphs which I now term Entitative Graphs. I shortly after abandoned that and took up Existential Graphs. The beta part and portions of the gamma part were in running order in a few months; but the work of completely systematizing the beta part was not a job to be hurried up,— or, at any rate, was not so as I conceive such work ought to be done. It was a ripening of corn, requiring the heat of hard work, indeed, but above all the ripening effect of time. Meantime, I have been making many and many an attack upon the gamma fortress, and have captured sundry redouts. Of course, I can work with it. But that only supposes such a degree of mastery as one has of a language when one can think in that language. How many people fancy that they know a language very well when they can think in it. If they pursue the study, they will afterward turn back and see that that was merely the time at which their real knowledge of the language was making its first beginning! It is precisely so in graphs. When you have learned to think in them easily without translation then you are ready to begin the real study of them.
512. The gamma part of graphs, in its present condition, is characterized by a great wealth of new signs; but it has no sign of an essentially different kind from those of the alpha and beta part. The alpha part has three distinct kinds of signs, the graphs, the sheet of assertion, and the cuts. The beta part adds two quite different kinds of signs, spots, or lexeis, and ligatures with selectives. It is true that a line of identity is a graph; but the terminal of such a line, especially a terminal on a cut where two lines of identity have a common point, is radically different. So far, all the gamma signs that have presented themselves, are of those same kinds. If anybody in my lifetime shall discover any radically disparate kind of sign, peculiar to the gamma part of the system, I shall hail him as a new Columbus. He must be a mind of vast power. But in the gamma part of the subject all the old kinds of signs take new forms.
If I were to expound to you fully the theoretically needed new forms of spots, cuts, and ligatures that are required in the gamma part, you would find the complexity of it,— presented in the hurried way that would be necessary,— to be not only tedious but also confusing.
It will be better to give you examples of what I have found most useful, and leave it to you to study out the rest if you care to do so. I shall have a printed syllabus ready for distribution at the next lecture which will be a great help; but even in that I cannot go into the long explanations that would be needed to expound the theory of the gamma part.
513. So far I have called the sheet a photograph, so as not to overwhelm you with all the difficulties of the conception at once. But let us rather call it a map,— a map of such a photograph if you like. A map of the simplest kind represents all the points of one surface by corresponding points of another surface in such a manner as to preserve the continuity unbroken, however great may be the distortion. A Mercator's chart, however, represents all the surface of the earth by a strip, infinitely long, both north and south poles being at infinite distances, so that places near the poles are magnified so as to be many times larger than the real surfaces of the earth that they represent, while in longitude the whole equator measures only two or three feet; and you might continue the chart so as to represent the earth over and over again in as many such strips as you pleased. Other kinds of map, such as my Quincuncial Projection which is drawn in the fourth volume of the American Journal of Mathematics, show the whole earth over and over again in checkers, and there is no arrangement you can think of in which the different representations of the same place might not appear on a perfectly correct map. This accounts for our being able to scribe the same graph as many times as we please on any vacant places we like. Now each of the areas of any cut corresponds exactly to some locus of the sheet of assertion where there is mapped, though undeveloped, the real state of things which the graph of that area denies. In fact it is represented by that line of the sheet of assertion which the cut itself marks.
514. By taking time enough I could develope this idea much further, and render it clearer; but it would not be worth while, for I only mention it to prepare you for the idea of quite different kinds of sheets in the gamma part of the system. These sheets represent altogether different universes with which our discourse has to do. In the Johns Hopkins Studies in Logic I printed a note of several pages on the universe of qualities,— marks, as I then called them. But I failed to see that I was then wandering quite beyond the bounds of the logic of relations proper. For the relations of which the so-called “logic of relatives” treats are existential relations, which the nonexistence of either relate or correlate reduces to nullity. Now, qualities are not, properly speaking, individuals. All the qualities you actually have ever thought of might, no doubt, be counted; since you have only been alive for a certain number of hundredths of seconds; and it requires more than a hundredth of a second actually to have any thought. But all the qualities any one of which you readily can think of are certainly innumerable; and all that might be thought of exceed, I am convinced, all multitude whatsoever. For they are mere logical possibilities, and possibilities are general, and no multitude can exhaust the narrowest kind of a general. Nevertheless, within limitations which include most ordinary purposes, qualities may be treated as individuals. At any rate, however, they form an entirely different universe from the universe of existence. It is a universe of logical possibility. As we have seen, although the universe of existential fact can only be conceived as mapped upon a surface by each point of the surface representing a vast expanse of fact, yet we can conceive the facts [as] sufficiently separated upon the map for all our purposes; and in the same sense the entire universe of logical possibilities might be conceived to be mapped upon a surface. Nevertheless, in order to represent to our minds the relation between the universe of possibilities and the universe of actual existent facts, if we are going to think of the latter as a surface, we must think of the former as three-dimensional space in which any surface would represent all the facts that might exist in one existential universe. In endeavoring to begin the construction of the gamma part of the system of existential graphs, what I had to do was to select, from the enormous mass of ideas thus suggested, a small number convenient to work with. It did not seem to be convenient to use more than one actual sheet at one time; but it seemed that various different kinds of cuts would be wanted.
515. I will begin with one of the gamma cuts. I call it the broken cut. I scribe it thus
This does not assert that it does not rain. It only asserts that the alpha and beta rules do not compel me to admit that it rains, or what comes to the same thing, a person altogether ignorant except that he was well versed in logic so far as it is embodied in the alpha and beta parts of existential graphs, would not know that it rained.
516. The rules of this cut are very similar to those of the alpha cut.
Rule 1. In a broken cut already on the sheet of assertion any graph may be inserted.
Rule 2. An evenly enclosed alpha cut may be half erased so as to convert it into a broken cut, and an oddly enclosed broken cut may be filled up to make an alpha cut. Whether the enclosures are by alpha or broken cuts is indifferent.
Consequently
is transformable into
So if we start from
equivalent to
the simple denial of g.
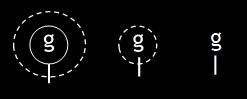
517. It must be remembered that possibility and necessity are relative to the state of information.
Of a certain graph g let us suppose that I am in such a state of information that it may be true and may be false; that is I can scribe on the sheet of assertion
ceases to be true; and518. You thus perceive that we should fall into inextricable confusion in dealing with the broken cut if we did not attach to it a sign to distinguish the particular state of information to which it refers. And a similar sign has then to be attached to the simple g, which refers to the state of information at the time of learning that graph to be true. I use for this purpose cross marks below, thus:
These selectives are very peculiar in that they refer to states of information as if they were individual objects. They have, besides, the additional peculiarity of having a definite order of succession, and we have the rule that from
we can infer
.519. There is not much utility in a double broken cut. Yet it may be worth notice that Fig. 181 and
and 520. It becomes evident, in this way, that a modal proposition is a simple assertion, not about the universe of things, but about the universe of facts that one is in a state of information sufficient to know.
without any selective
.521. Now suppose we wish to assert that there is a conceivable state of information in which the knower would know g to be true and yet would not know another graph h to be true. We shall naturally express this by
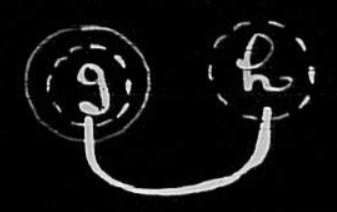
Here we have a new kind of ligature, which will follow all the rules of ligatures. We have here a most important addition to the system of graphs. There will be some peculiar and interesting little rules, owing to the fact that what one knows, one has the means of knowing that one knows,— which is sometimes incorrectly stated in the form that whatever one knows, one knows that one knows, which is manifestly false. For if it were the same to say “A whale is not a fish” and “I know that a whale is not a fish,” the precise denials of the two would be the same. Yet one is “A whale is a fish” and the other is “I do not know that a whale is not a fish.”
522. The truth is that it is necessary to have a graph to signify that one state of information follows after another. If we scribe 
to express that the state of information B follows after the state of information A, we shall have
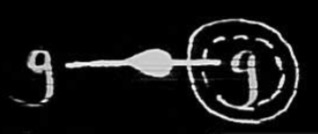
523. It is clear, however, that the matter must not be allowed to rest here. For it would be a strangely, and almost an ironically, imperfect kind of logic which should recognize only ignorance and should ignore error. Yet in order to recognize error in our system of graphs, we shall be obliged still further to introduce the idea of time, which will bring still greater difficulties. Time has usually been considered by logicians to be what is called “extra-logical” matter. I have never shared this opinion. But I have thought that logic had not reached that state of development at which the introduction of temporal modifications of its forms would not result in great confusion; and I am much of that way of thinking yet. The idea of time really is involved in the very idea of an argument. But the gravest complications of logic would be involved in so far taking account of time as to distinguish between what one knows and what one has sufficient reason to be entirely confident of. The only difference, that there seems to be room for between these two, is that what one knows, one always will have reason to be confident of, while what one now has ample reason to be entirely confident of, one may conceivably in the future, in consequence of a new light, find reason to doubt and ultimately to deny. Whether it is really possible for this to occur, whether we can be said truly to have sufficient reason for entire confidence unless it is manifestly impossible that we should have any such new light in the future, is not the question. Be that as it may, it still remains conceivable that there should be that difference, and therefore there is a difference in the meanings of the two phrases. I confess that my studies heretofore have [not] progressed so far that I am able to say precisely what modification of our logical forms will be required when we come to take account, as some day we must, of all the effects of the possibilities of error, as we can now take account, in the doctrine of modals, of the possibilities of ignorance. Nor do I believe that the time has yet come when it would be profitable to introduce such complications. But I can see that when that time does come, our logical forms will become very much more metamorphosed by introducing that consideration than they are in modal logic, where we take account of the possibility of ignorance as compared with the simple logic of propositions de inesse, as non-modal propositions in which the ideas of possibility and necessity are not introduced are called.
I will here take leave of this department of the gamma graphs in order to consider another. Instead of saying that opium puts people to sleep we may say that opium has a dormitive virtue. In that particular case little or nothing is gained by the more complicated expression. But in some cases there is a great gain. When, for example, instead of saying that a particle moves we say that the particle describes a line we introduce an abstraction in the same manner as when we talk of a dormitive virtue. But the advantages here are manifest, since we may imagine a filament to occupy the whole line at once, and we may further imagine that that filament moves in such a manner that at each moment it altogether quits the line which it is momentarily occupying. Here again we may introduce an abstraction and say that the filament generates a surface. Then we may imagine a material film to occupy the whole surface at once, and may imagine that the film moves in such a way that at each moment it is quitting the surface at which it is just arriving; and if it is not restricted to the space of our ordinary intuition we may say that the character of its motion determines a particular space, tridimensional at each point of it. This space, probably much more peculiar than the simple space we know, might, for aught we can see, be occupied all at once by a body. And we cannot see why this body should not move so that at every instant it should altogether quit the space that it at that instant occupies; and so on.
Here we see that the introduction of abstractions has led us to conceptions some of which, at any rate, are of the highest value. The others teach us still more if it can in any way be shown that they are impossible, and how they are so.
Hegel, I suppose, would regard a point as far more abstract [than] three dimensional space. This is, according to my principles of terminology, an abusive, or at any rate, an unadvisable use of the word abstraction. But what Hegel means is that it is nearest to experience in its totality. In the case of space we pass backward in this way. Here is a glass object. Everything isn't glass. There is besides air. No air is glass. There is however something no part of which is altogether glass and no part altogether air. It is glass-air. This is the surface between the glass and the air.
Now we place a little water against a part of that surface. There are now three surfaces, one of glass-air, a second of glass-water, a third of air-water. There is some thing that is, in the same sense, between the glass-air surface and the glass-water surface; and this must necessarily also be between either of those and the water-air surface. It is the line where glass air and water meet. Now let us put a piece of putty over a portion of that line. There are now three additional surfaces, the putty-glass surface, the putty-air surface, and the putty-water surface, and there are three additional lines, the putty-glass-air line above, the putty-glass-water line below, the putty-air-water line on the level surface. These four lines all come together at some even number of different points.
I will not stop to explain the metaphysical explanation of our coming out with an even number of points except in peculiar cases when two of them coincide, but will merely say that it is owing to pure space being of the nature of a law, while a body in space has individual existence; now existence is an affair of Secondness, and thence it would be found, upon minute analysis, to be necessary that if anything exists there should exist something else, upon which it may react; and in order that the law of space should not unite the two things a twofold condition has to be satisfied from which it results, I will not stop to explain how, that the points reached should be two.
Here is a logical proportion:
| A particle moves | A pear is ripe |
| A particle passes over a path | A pear possesses ripeness |
| A filament moves from its place | Ripeness is more or less |
| A filament passes over a surface | Ripeness possesses degree |
525. It is obvious that the lines of identity on the left-hand side of the potentials are quite peculiar, since the characters they denote are not, properly speaking, individuals. For that reason and others, to the left of the potentials I use selectives not ligatures.
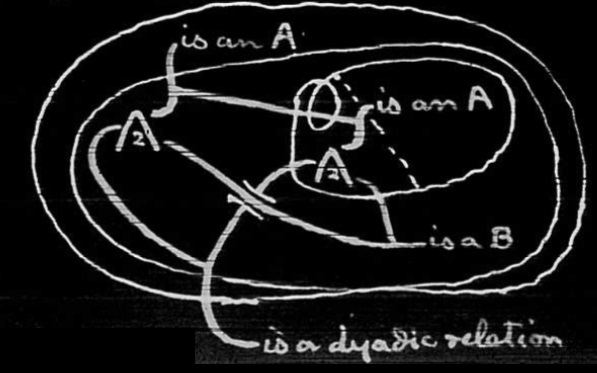
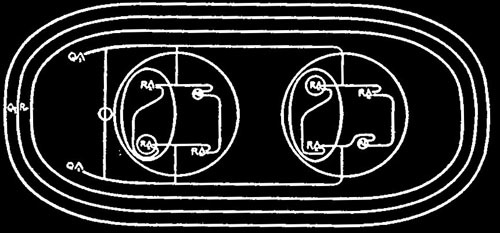
526. As an example of the use of the potentials, we may take this graph, which expresses a theorem of great importance: The proposition is that for every quality Q whatsoever,
527. I will now pass to another quite indispensable department of the gamma graphs. Namely, it is necessary that we should be able to reason in graphs about graphs. The reason is that a reasoning about graphs will necessarily consist in showing that something is true of every possible graph of a certain general description. But we cannot scribe every possible graph of any general description, and therefore if we are to reason in graphs we must have a graph which is a general description of the kind of graph to which the reasoning is to relate.
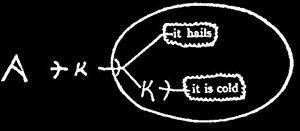
528. For the alpha graphs, it is easy to see what is wanted. Let 
, the old Greek form of the letter A, denote the sheet of assertion. Let —γ is a graph. Let Y-b.jpg)
X mean that X is scribed or placed on Y. Let W–k–Z mean that Z is the area of the cut W. Let U–
mean that U is a graph, precisely expressing V. It is necessary to place V in the saw-rim, as I call the line about it, because in thus speaking of a sign materialiter, as they said in the middle ages, we require that it should have a hook that it has not got. For example
, wherever it occurs,
.
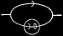529. We come now to the graphical expressions of beta graphs. Here we require the following symbols,
| XY | means Y is a ligature whose outermost part is on X. |
 | means g is expressed by a monad spot on X whose hook is joined to the ligature Y on X. |
 | means g is expressed by a dyad graph on X whose first and second hooks respectively are joined on X to the ligatures Y and Z. |
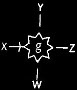 | means g is expressed by a triad graph on X whose first, second, and third hooks are joined on X to the ligatures Y, Z, W, respectively. |
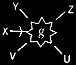 | means g is expressed by a tetrad spot on X whose first to fourth hooks are joined to Y, Z, U, V, respectively. |