Lowell Lecture 5 of 1903 (MS 468-71)

transcribed and edited by Gary Fuhrman, April-May 2018, from the manuscript copies made available by the SPIN project (link above). This is a provisional transcription designed for continuous reading of the lecture in something like the way that Peirce presented it, omitting parts that seem to be fragmentary. I have also added some punctuation for the sake of clarity. Where the order does not follow that of the manuscript pages as reproduced on the SPIN (FromThePage) site, I've provided some links to the manuscript pages themselves, to facilitate comparing them with my transcription.
Most of this lecture has been previously published in NEM 3, 365-391. Part of it was also included in Matthew Moore's 2010 selection of Peirce's writings on Philosophy of Mathematics (PM, 100-105).

[MS 469]

Lowell Lectures 1903

Lecture 5 Vol 1

Ladies & Gentlemen:

[MS 470 p. 124]

I am going to speak to you tonight about multitude or maniness and shall, I hope, be able to give you a glimpse of its logical importance. Some kinds of infinity will come under our notice, but I fear I shall not have time to speak of other kinds. I shall say a few words only concerning continuity. All of these subjects become intensely interesting and of great importance if one can go into them in some detail. But the difficulty with a course of this kind is that it is not possible to go deeply enough into the subjects to reach the really valuable parts of them.

I must begin by a few words concerning gramma graphs; because it is by means of gamma graphs that I have been enabled to understand these subjects, and I do not believe it is possible really to understand them except by some method equivalent to that of gamma graphs.

In particular, it is absolutely necessary to representing the reasoning about these subjects that we should be able to reason with graphs about graphs and thus that we should have graphs of graphs.

It is essential to a graph or any other expression of a proposition that it should be represented by its interpretant sign to be true. But to say that it is true implies that it really is affected by its object; and in order that this object should have a real effect upon it, this object must be a subject of force, which is an individual. Consequently, an adequate interpretant of a graph must represent it as a sign of an individual. How, then, can there be a graph of a graph, considering that a graph is a legisign, or sign which has the mode of being of a general type, just as any word is a general type, and not a single individual object in a single definite place at a single instant. The answer is that a graph can only have a graph for its object indirectly. Directly, it can only refer to a graph replica. But it can assert what it asserts of any graph-replica you please so long as it be equivalent to a given graph replica.

The matter is unsuitable to presentation in a course like this, although it is indispensible that something should be said about it. If I can ever get the funds to print it, I shall be very happy to send copies to all who may care for them.

This matter of the graphs, if I could present it, would also illustrate the nature of Pure Mathematics, still better than it is illustrated on pages 20 to 22 of the Syllabus distributed last Thursday. Mathematics, in general, is tbe science of the logical possibility and impossibility of hypotheses. Upon that definition first put forth by my father Benjamin Peirce in 1870, mathematicians are now pretty unanimously agreed. Pure mathematics differs from mathematics in general in not admitting into its hypotheses any element that does affect their logical possibility or impossibility. Thus, the pure mathematics of graphs, as you see in those pages of the syllabus, says nothing at all about the logical interpretation of graphs but defines them exclusively by their logical relations to one another. So the pure mathematical presentation of graphs of graphs says nothing at all about the graphs considered being representations of graphs, but merely defines the graphs representing the sheet of assertion, a cut, its area, a line of identity, and so forth, in terms of their logical relations to one another.

The theory of graphs of graphs rests upon a larger number of independent hypotheses than do most branches of pure mathematics. I divide these hypotheses into those which relate to physical possibilities and necessities and those which relate to permissions and prohibitions. The former class, about thirty in number, are all expressible in alpha and beta graphs. The latter class, which do not much exceed half a dozen, require, one and all of them, gamma graphs to express them. In particular the broken cut enters into every one, and into some of them with curious complications.

One is surprised to find how extremely complicated are the graphs that express some of these fundamentals of the nature of graphs; and this complication puts into a strong light two merits of this system of existential graphs. For, on the one hand, it shows the extraordinary analytical power of the system that analyzes conditions which seemed on our first acquaintance with them to be very very simple but which the system of graphs forces us to see are in reality very complex; while on the other hand, this same complication shows that the system of existential graphs possesses to an extraordinary degree the virtue that belongs more or less to all diagrams, that of putting a matter really extremely complicated into a light under which it is fully and adequately represented and yet seems as easy and natural as slipping off a floating log.

[MS 469 p.2]

But I must hasten to the subject of numbers.

Whole numbers can on the one hand be studied in two ways which are surprisingly different from one another throughout. They can be studied as qualities of collections, making the members of one collection many and those of another few, which is called by the Germans, with their usual incapacity for language, the doctrine of Cardinal Numbers; but which ought to be called the doctrine of Multitude. Or, on the other hand, numbers may be considered simply as objects in a sequence, as ordinal numbers. The latter study is a branch of pure mathematics, because it makes no difference what kind of objects they are that are in series, nor whether it is a series in time, in space, or in logic. The doctrine of multitude, on the other hand, is not pure mathematics. For the objects it studies, the multitudes, are in a linear series exactly as the doctrine of ordinal numbers supposes; and since the doctrine of ordinal numbers permits the members of the series to be objects of any kind, it follows that it permits them to be multitudes. Thus the doctrine of multitude is nothing but a special application of the doctrine of ordinal numbers. But the special objects of its series have a special character which permits them to be studied from a special point of view; and that point of view is a logical point of view. It is not the pure mathematical forms that we study in the doctrine of multitude. It is on the contrary a branch of logic which, like all logic, is directly dependent upon mathematics.

The first question we come upon in the study of multitude is very obviously a purely logical question; and there is nothing at all corresponding to it in the doctrine of ordinal numbers: it is the question what is multitude. Multitude is obviously a relative quality of collections, or plurals. Therefore the question becomes, What is a collection? That is obviously a most important question for logic; and it is about as difficult a one as could be found. In speaking of a collection, we do not mean that its members are physically or in any way existentially brought together. We mean by a collection merely a plural, whose objects are collected together by thought. The collection exists just as much as its members. Their existence is its existence. Yet in another point of view it is the creation of thought. It is an ens rationis. An ens rationis may be defined as a subject whose being consists in a Secondness, or fact, concerning something else. Its being is thus of the nature of Thirdness, or thought. Any abstraction, such as Truth and Justice, is an ens rationis. That does not prevent truth and Justice from being real powers in the world without any figure of speech. They are powers, just as much, and in the same way, as I am a power if I can open my window should the air seem to me stuffy. A collection is an abstraction, or is like an abstraction in being an ens rationis. But it is unlike an abstraction in that it exists. Truth and Justice do not exist, although they are powers. I myself, properly speaking, do not exist. It is only a replica of me that exists, and I exist in that replica as the effect of my being as a law. A collection, however, exists, and this existence is derived from the existence of its members which may be pure Secondness. Our bodies are of course much more than so many collections of molecules; but as far as its existence is concerned, the existence of our bodies consists in the existence of the molecules. But the word collection and other words of the same general meaning have two different meanings with a very fine distinction between them. This makes a large part of the difficulty of defining a collection and the non-recognition of this distinction makes a serious stumbling block in the doctrine of cardinal numbers. In accordance with my views of the Ethics of Terminology, I am going to make two new words to distinguish these two meanings. The one I shall call a gath which is simply the word ‘gather’ with the last syllable dropped. The other I call a sam which is the word ‘same’ with the last letter dropped. I also like this word because it is so much like the word sum, in the phrase sum total. It also recalls the German word Samlung. A collection, in the sense of a gath is a subject which is a pure Secondness without Firstness, and whose only mode of being is whatever existence it may have; and this consists in the existence of certain other existents, or pure Seconds, called its members. Thus, the gath of human beings at this moment in Boston, consists in the existence of this man and that man. No matter how those men might be transformed, no matter if some of them were to leave Boston, that same gath exists, although it would cease to be the gath of the inhabitants of Boston. But were a single member of the collection to cease to exist, that gath would no longer exist. There would still be a gath of inhabitants of Boston but it would be a different gath. The description, ‘All the inhabitants of Boston’ describes a gath. But as time goes on it will describe a different gath.

The description ‘the inhabitants of Boston’ is a proper name. It applies to but a single individual object, the whole of all the inhabitants of Boston. This whole, what I call a Sam, is not exactly a gath; and it is important to get a distinct idea of the difference. Just as the molecules that compose a man's body are continually changing by the loss of some and the gain of others, while there remains the same man, so the population of Boston is ever changing, yet remains the same individual whole. I propose to say it is the same sam. But it does not remain the same gath. At each instant it is identical with a gath. Always there is a gath in the existence of which consists the existence of the sam of the inhabitants of Boston. Were the city to be devastated and not one inhabitant left, still, as long as it remained Boston, the ‘sam, or sum total, of the inhabitants of Boston’ would have a being, although it would under those circumstances have ceased to exist. It would continue to be, since the description would retain its meaning. The essence of the sam would remain, although its existence had departed. But as for the gath, since it has no other being than existence, and its existence consists in the existence of its members; and since under those circumstances no members would exist, the gath would altogether cease to be. It is important to have this distinction clearly in mind. I do not mean to say that [it] is usually important to hold this distinction clear in regard to any collection that we may happen to speak of; but I mean that for certain purposes it is indispensibly necessary. Whatever sam there may be to whose members, and to them alone, any sign applies, is called the breadth of the sign. This word breadth, originating with the Greek commentators of Aristotle, has passed into our vernacular. We speak of a man of broad culture. That means culture in many fields. Breadth of mind is the character of a mind that takes many things into account. If a man has broad and deep learning, the breadth consists in how many different subjects he is acquainted with, and the depth in how much he knows about whatever subject he is acquainted with. Now the breadth of a descriptive appellation has an essence, or Imputed Firstness, which is the signification, or Depth, of the appellation. Take the word phenix. No such thing exists. One naturally says that the name has no breadth. That, however, is not strictly correct. We should say its breadth is nothing. That breadth is precisely what I mean by a sam. Therefore I define a sam as an ens rationis having two grades of being, its essence, which is the being of a definite quality imputed to the sam, and its existence which is the existence of whatever subject may exist that possesses that quality. A gath, on the other hand, is a subject having only one mode of being which is the compound of the existence of subjects called the members of the gath.

You may remark that a sam is thus defined without any reference at all to a gath. I repeat the definition, so that you may observe this:

A sam is an ens rationis whose essence is the being of a definite quality (imputed to the sam) and whose existence is the existence of whatever subject there may be possessing that quality.

On the other hand, it is impossible to define a gath without reference to a sam. For when I say that a gath is a subject whose only mode of being is the compounded existence of definite individuals called its members, what is the meaning of this compounded existence. It is plain that the idea of a compound is a triadic idea. It implies that there is some sign, or something like a sign, which picks out and unites those members. Now the fact that they are all united in that compound is a quality belonging to them all and to nothing else. There is thus here a reference to a possible sam which does this. Thus, we might as well at once [have] defined a gath as a subject which has but one mode of being which is the existence of a sam. From this fact, that a gath cannot be defined except in terms of a sam, it follows that if by a collection be meant, as ordinarily is meant, a gath; while a gath is not distinguished from a sam, it becomes utterly impossible to define what is meant by a collection.

This would not be true if the two clauses of the definition of the sam were two distinct ideas which have to be put together; but it is not so. Secondness involves Firstness, although it can be discriminated from it; and consequently the idea of the existence of that which has an essence, which is simple Secondness, is a decidedly simpler notion than that of existence without essence, or a Secondness discriminated from Firstness. For it is only by a rectification applied to the former notion that the latter can be attained.

No doubt the easiest way to conceive of the sam is to imagine that you have a common noun, without specifying what noun it is, and to think that that noun signifies some quality which is possessed by anything to which it applies, but is not possessed by anything to which it does not apply. Now you are to imagine a single thing which is composed of parts. Nothing is done to these parts to put them into their places in the whole: their mere existence locates them in the whole. Now think of this rule as describing the whole. If any individual object can properly have that common noun predicated of it, it is a part of the single object called a sam; if not, it is not. That gives you the idea of the sam. Now to get the idea of a gath, you are to consider that those individual objects might change their qualities without losing their individual identity; so that limiting ourselves to any instant[,] any individual object which at that instant forms a part of the sam forever forms a part of an object of which no object not at that instant a part of the sam is a part, and this individual composite whole which has nothing to do with the qualities of its members is a gath.

For every gath there must be a corresponding sam. This is what we should ordinarily express by saying that whatever exists is possible. Or, as De Morgan put it, the individuals of whatsoever collection have some quality common to them all that is peculiar to them i.e. possessed by nothing else. Kant, I dare say, would remark that this is a Regulative Principle but that it cannot be proved to be a Constitutive principle. That is, it is proper to assume it, but you cannot prove it is so. But I reply that every principle of logic is a Regulative Principle and nothing more. Logic has nothing to do with Existence. And I should add: Herr Professor Dr. Hofrath Kant, permit me to say that in saying this is not a Constitutive principle you speak of qualities as if they were existent individuals. A quality has no other being in itself than possibility and to say that a quality is possible is to say that it has all the being that in the nature of things a quality could have. If as you say there may be a quality common and peculiar to all the members of a gath, then there certainly is such a quality; and you yourself have in this very same breath described one such quality, in saying that they are all members of the gath in question. So for every gath there is a corresponding sam. But it is not true that for every sam there is a corresponding gath. Since there is the sam of the phenix, although it happens not to exist up to date. But there is no such gath since there is no phenix. Another point which I observe puzzles the Hon. Bertrand Russell in his ‘Principles of Mathematics’ is whether a collection which has but a single individual member is identical with that individual or not. The proper answer is that if by a collection you mean a sam, the sam of the sun is not the sun, since it is an ens rationis having an essence, while the individual has no essence and is not an ens rationis. But if you mean the gath, the gath of the sun has no being at all except the existence of the sun which is all the being the individual existent sun has. Therefore, having precisely the same being they are identical and no distinction except a grammatical or linguistic one can be drawn between them. Mr. Russell's being puzzled by this is a good illustration of how impossible it is to treat of philosophy without making a special vocabulary such as all other sciences make. It is, however, far more needed in philosophy than in any other science, for the reason that the words of ordinary speech are needed by philosophy for its raw material.

What has been said of qualities is equally true of relations, which may be regarded as the qualities of sets of individuals. That is to say, if any form of relation is logically possible between the members of two given gaths, a relation of that form actually exists between them.

In order to illustrate this principle, I will consider a proposition which the ablest mathematicians have been endeavoring for half a century to demonstrate to be either true or false. The proposition assumes that there are two gaths, which we may call the A's and the B's. And now if we use the phrase a “one to one relation” to denote such a relation that no relate stands in that relation to two different correlates nor any two relates to the same correlate; like the relation of husband to wife in a monogamous country, or better of father to eldest child, then it is assumed that there is no one-to-one relation in which every B stands to an A. Then the question is whether there is necessarily any one to one relation in which every A stands to a B.

Since there is no one-to-one relation in which whatever B there may be stands to an A, it must be logically impossible that there should be any such relation. But since the form relation in itself is not absurd, and since in point of fact every B does stand in such a relation to some member of a gath, for every B stands in the relation of identity to some B, it follows that the logical impossibility lies in some existential limitation of the As. However, dropping at the outset the assumption about the one to one relation considering any two gaths, the As and the Bs, there is a relation in which no relate stands to two different correlates (though two relates may stand in it to the same correlate) in which every B stands to an A; for the Bs may so stand to any one A. Now setting out with such a relation, let us ask whether by a change of it so as to change each correlate into some other individual of the universe, it is possible so to change it as to make every A a correlate of it. Let us trace out the consequences of supposing this not to be possible. Let us under this hypothesis change our relation by a change of correlates so as to render it a one to one relation, and let us suppose this to be done in every possible way so as to give a vast multitude of different one to one relations. Among these different relations there must be some all of whose correlates are A's because every possible variation of our relation occurs, and they could not all agree in any respect unless it were logically compelled. But since we are going on the hypothesis that every one of these relations leaves some A that is not a correlate, it follows that there is nothing to compel any correlate to be non-A; for the only logical requirement is that no two correlates shall be identical and since even when we do not care whether they are so or not there are A's that are non-correlates, it follows that there is nothing to compel any correlate to be a non-A, since there are A's that it may be.
[MS 469 p. 44]
But there cannot be any compulsion that does not affect any individual, and therefore there is nothing to compel correlates to be non-A's and consequently in some cases none will be non-A's. But now if we bring in the assumption that there is no one-to-one relation in which every B stands to an A, this result is rendered impossible, and with it disappears the hypothesis of which it is a necessary consequence; namely, that there is no relation in which no relate has two correlates and in which some B stands to every A. This hypothesis being overthrown it appears then that there is such a relation in which no B stands to two A's yet of which every A is correlate to some B. But we have only to exclude from this all but one of the relations of different B's to the same A for every A to reduce its converse to a one-to-one relation of every A to a B. Thus we have proved that if there is no one to one relation of every B to some A there is a one to one relation of every A to some B.

Let us now look into another problem. Dr. Georg Cantor has a wonderful system of Ordinal Numbers which I must explain to you. It begins with the ordinary ordinal numbers
1, 2, 3 4 5 6 7 8 9 10 11 ...
That series is endless. That is to say, it has no last. But neither in logic nor in fact does that interfere with its being gone completely through provided the objects numbered are not in the nature of existences. When for instance Achilles runs after the Tortoise and we choose to divide his course into a first stage in which he goes to the place where the tortoise was at first, a second stage in which he goes to the place where the tortoise was at the end of the first stage, a third stage in which he goes to the place where the tortoise was at the end of the second stage, and so on, the series of stages is endless. But nothing in logic, or in fact, prevents Achilles from accomplishing them all, since they are only possibilities. So then there will be other ordinal numbers, after the first endless series is gone through. And the first of these Cantor denotes by ω, then every ordinal number having one next after it, the series runs
ω+1, ω+2, ω+3, ω+4, ω+5,
and after this endless series is accomplished then will come ω+ω which he calls ω·2
Then according to the rule must come
ω·2, ω·2+1, ω·2+2, ω·2+3
ω·3, ω·3+1
ω·4
ω·5 etc.

This series ω, ω·2, ω·3, ω·4, ω·5 is endless and after it is accomplished we shall have ω·ω or ω². Then
ω², ω²+1, ω²+2
ω²+ω
ω²+2ω and so on
ω²+ω² = ω²·2 and so at length ω³ ω⁴ ω⁵ and endless series, after which ω^ω. Then there will be

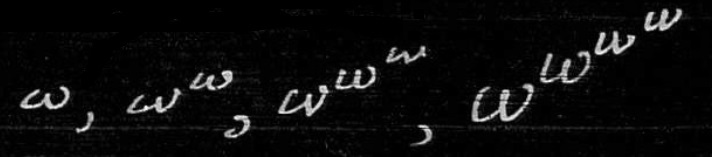
Cantor gives no other way of writing these. But Suppose that instead of ω² we write ω(1,2). For ω³ ω⁴, we write ω(1,3), ω(1,4). For ω^ω, etc. we write ω(1,1,2), ω(1,1,3). So that (ω^ω…)⁵·6 will be written ω(6·5·4). Then we shall at length get ω(1,1,ω) which may write ω(1,1,1,2). So we shall get w(1,1,1,1,2) w(1,1,1,1,1,2), w(1,1,1,1,1,1,2) and after all these we may put ω((1),2).

Then we shall have at length ω((1),(1),2) and so forth and then ω(((1))2) and so ω((((1)))2) ω(((((1))))2) and after that we may put w[2]. In short, there will be no end to the need of new symbols. It all follows from two principles, 1st, every number has another number next after it. 2nd, every endless series of numbers accurately describable in any manner whatever has a number next after it.

Cantor calls such a series a wohlgeordnet series. But I propose, in admiration of the genius that has discovered it, to call it a Cantorian succession. Cantor has conjectured that, given any collection whatever, any universe you please of independent quasi-individuals, there is a relation (and if one of course innumerable such) that in passing from relate to correlate and from correlate to correlate's correlate, this relation arranges the whole universe in a Cantorian collection.

Indeed, Cantor put forward this as more than a conjecture,— as a consequence of an unacknowledged law of thought. But the proposition has been received by mathematicians with the gravest doubt.

If I have time, I will say more about this very important question later; but at present I will only say this. The relation is per se possible. It only supposes that certain individuals shall have special one-sided connections. Now every two individuals have special one-sided connections. Neither can any limitation of existence render this form of relation self-contradictory. Therefore, Cantor is right. This cannot be clear to you. It is the merest hint. But I might give several lectures elucidating this matter. I must hurry on to other things.

Having made it clear what a collection is, the next thing I have to do is to define Multitude. If we regard plural nouns, such as men, horses, trolley-cars, as names describing sams, men meaning a sam of which any member is a man, etc.: then the adjectives two, ten, myriad, innumerable, express qualities of collections of a certain class, and any quality of this class is a multitude. Of course, this is not a definition. It is only the framework for a definition. In order to define multitude, it is necessary to begin by analyzing our meaning when we say that one collection is greater than another. This analysis was first published in a posthumous work of Bernard Bolzano, which appeared in 1851 and has since been reprinted Paradoxien des Unendlichen. Bolzano was a catholic theologian of Hungary and the author of a logic in four volumes. He was far too clearheaded to escape persecution in his position, you may be sure. Bolzano's definition amounts to this. If one gath, say that of the Bs, is so related to another gath, say the As, that there can be no one-to-one relation in which every B stands to an A, then, and only then, the gath of the Bs is greater than that of the As, and the latter is less than the former. For example there is no possible one-to-one relation in which every one of five things stands to one of three things.

Then it follows from the proposition I proved a little while ago that one collection cannot be at once greater and less than another. It may however be neither greater nor less.

On Balzano's definition of greater and less can be based a definition of Multitude. That is the multitude of a collection will be defined as consisting in its being greater than those collections that [it] is greater than and being less than those it is less than. This definition is at least a practicable one. It can be put to use in demonstrations. In that respect it is infinitely better than what Cantor puts forth as a definition in the style of Kant, who was a superb logical genius but who never studied logic and therefore sometimes commits grievous faults of logic. Namely Cantor tells us that if we think of a collection and then put out of view this and that element of our idea, what remains is multitude. But that is no definition at all. It is an experiment telling us, granting for the sake of argument that it attains its aim, how to find and identify multitude. A definition ought to be an analysis of a conception useful in demonstration. The purely relative definition based on Balzano's definition of greater and less does that. But it takes too narrow and formal a view of the matter. It fails to show the immense logical significance of multitude. It also makes it to be a purely relative between one collection and others. That is not true. The multitude of a collection would be just what it is if there were no other collection in the world. Let me offer a definition. The multitude of a gath,— remember, it is a pure gath and the special firstnesses or flavors of the characters of its units and sets of units is put out of the question,— consists in the complexity of the relations existing between its units in virtue of its peculiar character purely as a gath. But what is meant by the complexity of relations? What does it consist in? In order to bring this home to you I compare a greater collection with a smaller. Among the units of any gath of multitude five or more there is the relation shown in this graph.

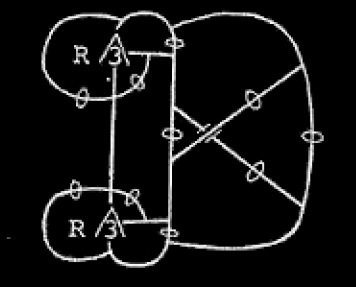
Now some logicians look upon every proposition as expressing a description of identity. That may be a contorted conception of a proposition, but it is not false. Adopting it for the moment, we see that the smallness of a collection compels descriptions of identities that in a larger collection are not compelled. But this is as much as to say that propositions follow as necessary consequences from premisses relating to members of smaller collections when in a larger collection no such conclusion would follow. If one collection is larger than another this will invariably be true. From this point of view you see the immense logical significance of multitude.

For instance, suppose you want to find out who committed certain murders, who some Jack the Ripper is. Plainly if you will be sure that he belongs to a certain small collection of persons your investigation may be greatly helped. You have ways of reasoning open to you that you had not before. Indeed if you can reduce the multitude of that collection to unity, your problem is solved.

Let us see then what all the different grades of multitude are. The lowest is unity for Nullity is not a multitude. Unity is that quality of a collection which consists in the absence of all diversity of its members. Add a single diverse individual to a collection of one, and you get a larger collection. Let me prove this by graphs. In each graph which I write, the universe of discourse [will] be the members of the gath I am dealing [with]. Then nullity will be expressed by which is of course the pseudograph. For a universe with nothing in it is absurd. I add one to this. That is I express that there is something such that if anything is different from this the graph of nullity holds for it. That is
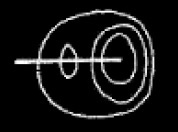or 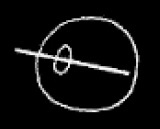. It is the graph of Unity. I add a unit to this. That is I express that there is something other than what the graph of unity asserts, but for all that is not this that graph holds. This gives
. It is the graph of Twoness. I again add a unit, asserting that there is something else but that apart from this new unit the graph of Twoness holds. This gives
which is the graph of Threeness. In order to express that the gath taken as the universe is greater than a given number you must assert all the diversity that the graph of that number asserts and also the diversity it denies. That is, we must remove the large cut. Then in order to assert that our gath is not [p. 72] more than the number we must enclose the last graph in a cut. Thus to express that that gath in question is more than three we have the graph
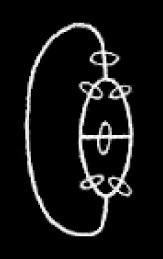. To assert that it is not more than three we scribe
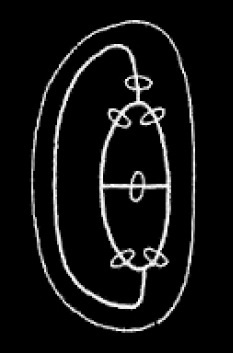. To assert that it is neither three nor more than three, that is that it is less than three, we scribe
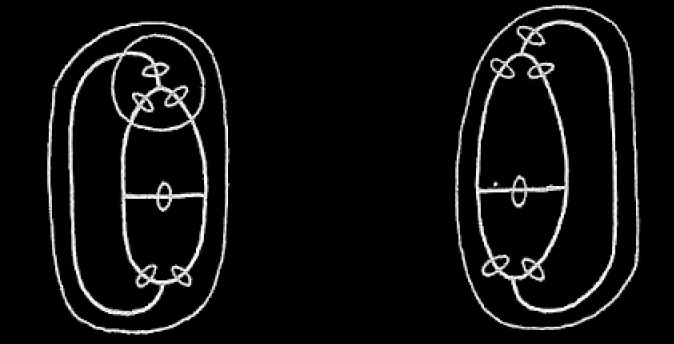. We now iterate the right hand graph in the second cut of the left hand one thus
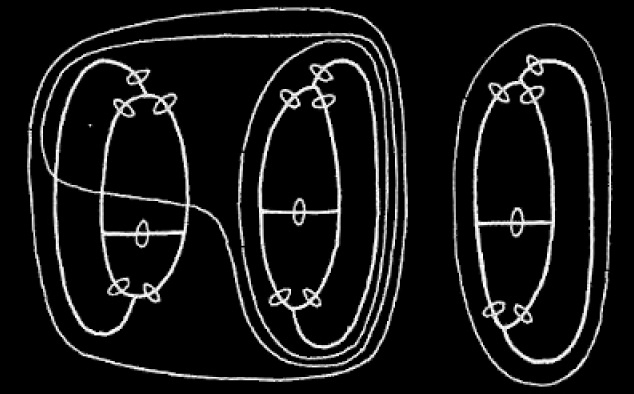
. We extend the ligature by the rule of Iteration and join them inside 3 cuts by the Rule of Insertion. We thus get, after erasing the left hand part,
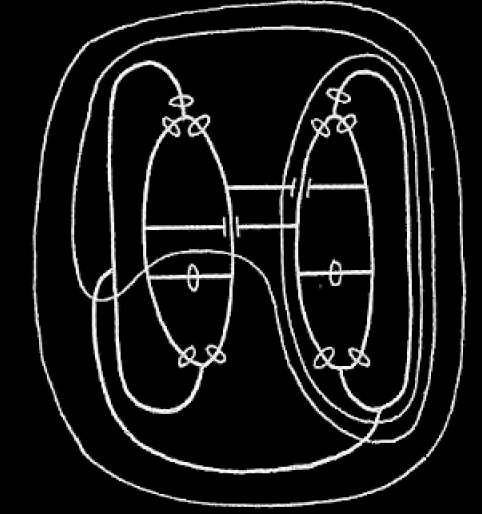. We now deiterate so as to get
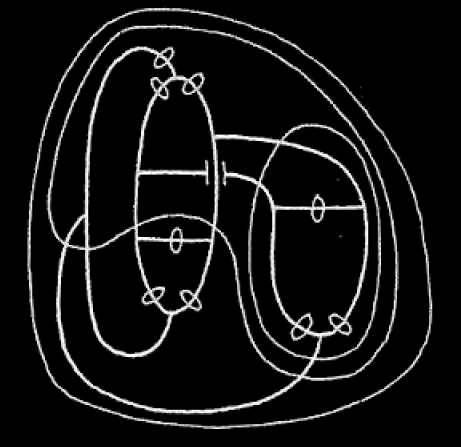. We erase within two enclosures giving
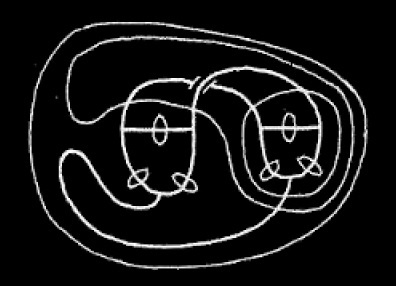. We remove the double cut getting
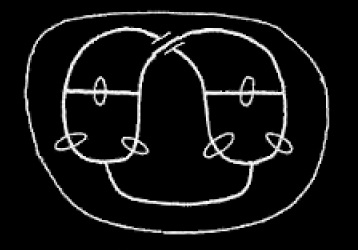and finally we deiterate getting
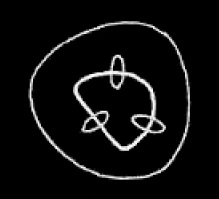. This signifies that the gath is not more than two. That is we have proved by graphs that there is no multitude intermediate between 3 and 2.

I am sorry there is no time to go further into the graphical treatment, because it becomes more and more interesting as we go on, and the results are very important. For instance, in order to prove by graphs that the Syllogism of Transposed Quantity holds good for all finite multitudes, since it is evidently impossible to scribe the graphs of all enumerable multitudes it is necessary to scribe a graph which shall describe what a graph of any enumerable multitude is like. The idea of a graph of a graph is in itself interesting. But it becomes far more so when we see what the character of that graph must be. In that way it can be proved what is, I confess, pretty plain, without the graphs that the smallest multitude that is greater than all finite multitudes is the multitude of a sam for which there is some relation, [MS 470 p. 92] and some individual unit of the sam, such that whatever quality there may be that is possessed by that particular unit, that quality being of such a nature that if it be possessed by any unit, say M, it is necessarily possessed by a unit in that particular relation to the unit M,— any quality I say of which these two propositions hold is necessarily possessed by every member of the collection. This is the property of the denumeral multitude which is made use of in Fermatian reasoning, a mode of reasoning that was invented by Pierre de Fermat, who was born in 1601 and died in 1666, and who was probably the greatest mathematical genius that ever lived. He also invented the mode of reasoning of the differential calculus. Fermatian reasoning has to be used in order to prove, rigidly prove, almost any proposition about whole numbers.

For example, in order to prove X + Y = Y + X whatever whole numbers X and Y may be, we first prove that it is so when Y = 1. That is we first prove X + 1 = 1 + X. To prove this we begin by remarking that it necessarily is so when X = 1. For then it is merely 1 + 1 = 1 + 1. Now suppose it to be true of any whole number N that N + 1 = 1 + N. Then it is true also of 1 + N. That is (1 + N) + 1 = 1 + (1 + N). For (1 + N) + 1 = 1 + (N + 1). I suppose that to be proved already. And since N + 1 = 1 + N, 1 + (N + 1) = 1 + (1 + N). So then X + 1 = 1 + X if true for any one value of X is true of the next greater value. But it is true when X = 1. Hence it is true for all values. Now then suppose X + Y = Y + X is true when Y has a particular value say N. That is suppose X + N = N + X. Then it will also be true when Y = 1 + N. That is X + (1 + N) = (1 + N) + X. For X + (1 + N) = (X + 1) + N and X + 1 = 1 + X as we have just proved so that

We call a collection of the members of which the Syllogism of Transposed Quantity necessarily holds an enumerable collection and one of which this is not true or where there is a Fermatian relation a denumeral collection,— in German abzählbar. [I]t follows that it is true of every enumerable collection.

All the whole numbers, properly so called, that is, all numbers of which our system of so called Arabic notation affords a definite symbol,— all the numbers up to any one form an enumerable collection. But the entire collection of whole numbers capable of representation in that system is a collection not enumerable, but innumerable. And the single multitude of all the whole numbers, or of any such endless series of which all the members up to any member form an enumerable collection is called the denumeral collection, “abzählbar” in German. The denumeral multitude is a single multitude of the class of innumerable multitudes.
[MS 470 p. 78]

I was saying that all collections less than a given collection can be reasoned about in ways that greater collections cannot. The mode of reasoning which is applicable to all enumerable collections, but to no others was first discovered, or first put into a logical treatise, by Augustus DeMorgan. He called it the syllogism of transposed quantity. Here is an example:

Every dollar borrowed requires a borrowed dollar to be paid out

No borrowed dollar paid out covers more than one dollar borrowed

∴ Every dollar borrowed has to be paid out.

Now I need not tell you that sundry business schemes are based on the idea of evading this conclusion. The notion is that dollars borrowed can partly be spent and can all be paid out by means of new dollars borrowed. It was at the great fire of 1835 in New York, if I remember rightly that this scheme first emerged. All the insurance companies declared themselves bankrupt except only the Etna of Hartford which advertised that it would pay all losses. It had not the money to do so; but its advertisement brought so many new policies that it did pay, and laid the foundations of a great future. Paying out of the increase of one's business is, of course, fatal in the long run. And yet after all that is what we are all doing. A young man marries without having the money in the bank to support a dozen children. It is not in accordance with sound business; but the human race would progress little if they did not bank upon the future. But restricting myself to teaching logic, I limit myself to saying that the syllogism of transposed quantity is valid for every enumerable universe and for such alone. Here is a specimen of this reasoning applied to a question of philosophy:

No second of past time was immediately followed by two different seconds of past time.

But the last second of past time has no second of past time immediately following it.

Hence there must have been some second of past time that did not follow any second, that is time must have had an absolute beginning.

Whatever definitely exists or has existed forms an enumerable collection, and the reasoning about time must be accepted so long as you suppose the passage of seconds to be so many events that actually did take place. The past and the future stand upon an altogether different footing in this respect.

The entire collection of all whole numbers is not enumerable, since if we prefix zero to them, the resulting series has zero for its first, one for its second, two for its third member and so on, and has no capacity for diversity greater than that of the collection of whole numbers without the zero.

From a denumeral collection, such as that of the whole numbers, you may take away, not merely an enumerable part, but a denumeral part, equal to the whole, without thereby making the whole less.

Thus from all numbers, take away all the odd numbers, and the remaining collection of even numbers is equal to the whole, since corresponding to every number N there is a distinct and separate even number, its double. So likewise the multitude of powers of ten, or numbers written by a single figure 1, followed by zeros 1, 10, 100, 1000, 10000, etc. is just as great as that of all whole numbers.

The multitude of rational fractional values is denumeral, since any one may be reached in one way of writing them one by one. Namely, we begin with writing
0/1                 1/0
which are not properly rational fractional values, and now we proceed by the following rule. Having gone through the row, go through the whole row again, and insert between each successive pair of fractions a fraction having for its numerator and denominator respectively the sum of the numerators and the sum of the denominators of the two fractions between which it is inserted. Thus we get successively

What is true of all fractional values is equally true of all fractions. They can also be written down in the order of their values one by one, and that without even performing any addition.

The entire collection of all the objects of thought however minute to which men's attention has ever been attracted or ever will have been attracted is enumerable. It is a definite finite number. The entire collection of all the exact objects of thought that ever will interest men in the endless future is denumeral.

But we shall soon see how inexpressibly few are the objects of a mere denumeral collection compared with the infinitely overwhelming majority of innumerable multitudes.
[MS 470 p. 98]

Now in order to make out what the higher multitudes are, it will be necessary for me to prove to you a proposition which I was the first to enounce and to prove. The proposition is this.

Take any gath whatever, whether it be enumerable or innumerable, and call its units the Ms. Now I am going to describe a sam which I call the exponential of the Ms. Every member of this sam called the exponential of the Ms is itself a sam composed exclusively of Ms and this exponential sam comprises among its members every sam that is composed exclusively of Ms.

For example suppose the Ms are only four, say M1, M2 , M3, M4. Then the exponential of the Ms will be the sam whose single members are these sams

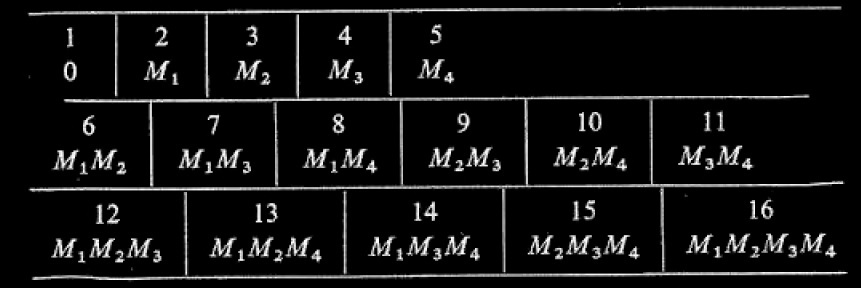
Now my proposition is that, in every case, the multitude of the exponential is greater than that of the primitive gath. That is, no matter what the Ms may be they are always fewer than all the possible sams of Ms. That is, it is impossible to find any one-to-one relation such that every sam of Ms stands in that relation to an M. How am I going to prove this? I do it in this way: I say, imagine any one-to-one relation you please, and call this the relation r. Now I will exactly describe a sam of Ms which does not stand in that relation, r, to any M whatsoever. You might suppose it would be difficult to describe so exactly a sam of Ms for which this relation fails when we know nothing at all about this relation except that it is a one-to-one relation called r. Nevertheless I will describe a sam of Ms which does not stand in the relation r to any M at all. I will call it my test sam. This test sam shall be composed as follows. Whether or not it includes among its members any particular M, say M_x, depends upon what kind of a sam of Ms it is that is in the relation r to M_x. It may be that there is no sam of Ms in the relation r to M_x. In that case, I do not care whether M_x be included in my test sam or not. But if there be a sam of Ms that stands in the relation r to M_x then if this sam of Ms includes M_x, M_x shall be excluded from my test sam, while if the sam of Ms that stands in the relation r to M_x does not include M_x as a member of it, M_x shall be a member of my test sam. That describes precisely my test sam except as regards certain possible Ms which may be all included or all excluded or some included and some excluded as you please.

Anyway I say that this test-sam does not stand in the relation r to any M. For take any M you please, I care not what. Call this M_y. Now M_y belongs to one or other of three classes; namely 1st, the class of Ms which I positively require my test sam to include, or 2nd, the class of Ms which I require my test sam to exclude, or 3rd, the class of Ms as to which I do not care whether they be included in the test sam or not. If M_y belongs to the first class, it is one of the Ms that I require my test sam to contain. But those were the Ms that were not contained in the sams of M that were r to them. Plainly then if M_y belongs to this class my test sam is not r to it. For my test sam, in this case, contains M_y, while the only sam of Ms that is in the one-to-one relation r to M, does not contain M_y. So this sole sam of Ms that is in the relation r to M, is not my test sam. If M_y however belongs to the second class, it is one of those Ms which I expressly exclude from my test sam. It is however contained in the only sam of Ms that stands in the relation r to it. Plainly, then, this sam that alone is in the relation r to M_y if M_y belongs to the second class is not my test sam. The only remaining possibility is that M_y belongs to the third class. But in that case it is one of these Ms to which no sam of M stands in the relation r; so that my test sam cannot stand in that relation to it. Thus you perceive that to whatever class M_y belongs my test sam cannot stand in the relation r to it. That is, as I said, I have specified a sam of Ms that does not stand in the one-to-one relation r to any M, no matter what that one-to-one relation may be. But that is as much as to say that the exponential of the Ms or the sum of all sams of Ms is more multitudinous than the gath of Ms.

Therefore, the collection of all possible collections of whole numbers is greater in multitude than the whole collection of whole numbers. I will show you an instance of such a collection. You know the secundal system of arithmetical notation, I am sure. It runs like this

1 one

10 two

11 three

100 four

101 five

110 six

etc.
So for the fractions

.1 is one half

.01 is one fourth

.11 three fourths

.001 one eighth

.011 three eighths

.101 five eighths

.111 seven eighths
and so on. Now consider all the values to which such fractions carried out indefinitely far could indefinitely approximate to.

The fractional places, being numbered correspond to the whole numbers. Those of these places that have ones in them are those which make up the whole collection of these places used to express the quantity. You see instantly, I am sure, that the entire collection of values to which such fractions can indefinitely approximate precisely corresponds to all possible collections of whole numbers. Such a collection I called in my paper abnumeral. But that is a poor word, and since it has not yet been taken up that I am aware of, I will call it the first ultranumerable multitude. Cantor calls it aleph 2, though he does not define it in the same way. It is the multitude of all possible points that could be marked on a line without putting any two at an infinitesimal distance from one another. It is the multitude of all the quantities that the differential calculus and theory of functions consider.

But now consider the multitude of all possible collections of such objects. That will be the second ultranumerable multitude, and there will be an endless series of infinite multitudes each greater than the last.

This series of multitudes is endless. That is there is no largest. But that does not in the least prevent there being a multitude greater than them all, just as the multitude of all whole numbers is greater than each whole number though there is no largest whole number. What then would come next? Collections of each of these multitudes is possible, notwithstanding that the least of the ultranumerables far exceeds the multitude of all the atoms in the universe. Still a collection of any ultranumerable multitude not only is possible but it really IS, in the sense in which any plural is apart from its having ever been thought of as such. Now, then, let collections of all these multitudes be aggregated. What sort of a collection will that be? It is easy to answer that question infallibly, though not so easy to comprehend the answer. The aggregate of those collections would falsify my proposition that the collection of collections of the Ms is greater than the Ms. It would not be so for such an aggregate. But that has been proved to be necessarily true for all collections. Then such an aggregate would not be a collection. It would be too many to be a collection. How so? I haven't time to show you; but I will tell you. It is because you have then so crowded the field of possibility, that the units of that aggregate lose their individual identity. It ceases to be a collection because it is now a continuum.

I regret exceedingly that I cannot give you a lecture on continuity because my discoveries in that field are of quite a different order of importance than those about multitude. I foresee that I shall die without getting my say said, although I strain every nerve in my work. The world will have to wait, I fear, a good while for the explanation of continuity if my work is not made public.

In the few minutes that remain I give you one or two scraps; but they are perfectly useless without the whole. One might as well, when a battle-ship is wanted, bring a quarter of a pound of boiler-iron.

I have in these lectures no concern with metaphysics. That is not saying that what I say has no importance for metaphysics. But for present purposes I care not what the real nature of time and space may be. But what I mean by a truly continuous line is a line upon which there is room for any multitude of points whatsoever. Then the multitude or what corresponds to multitude of possible points,— exceeds all multitude. These points are pure possibilities. There is no such gath. On a continuous line there are not really any points at all. Two lines which intersect, intersect in a point. That is true for the intersection breaks the continuity and makes a point where there was none before the intersection.

[MS 471]

transcriber's note: It is not clear (to me anyway) how the content of MS 471 is related to the rest of Lecture 5. It can't be the conclusion of the lecture, and it doesn't seem to fit anywhere into the text given above. It may be an earlier draft of the lecture or part of one. It is included here, despite some repetition of the content above, for the sake of some content which differs from the above (for instance, remarks about the relation between generality and indefiniteness).

I have now said all I need say about rationals. It is plain that in order to consider analytic continuity I must take up irrationals. I shall not need to consider any other ordinal. In order to consider true continuity I must consider the doctrine of multitude; and it will be more convenient to consider multitude first and irrationals afterward.

But at the very threshold of multitude, I am met by a great logical difficulty. For the whole doctrine of Multitude is founded upon a conception of the relation of one collection's being greater than another which is by no means the common-sense idea of that relation and which was first given to the world by Bernard Bolzano, who was at once a logician and a catholic theologian, a combination of specialties pretty sure to lead to grave personal inconvenience, as it did in his case and has done in most cases where the logician has attempted to advance his science. The common sense idea of being greater than is that if one collection contains a member representative of every member of another collection and more beside, it is greater than that other; and consequently an infinite collection is greater than itself. But Bolzano's definition does not allow any collection to be greater than itself, if there are two collections the As and the Bs and if there is any possible relation, r, in which every A stands to a B to which no other A is r, then, says Bolzano, we will say that the collection of A s is not greater than that of the B s. If there be no possible relation of that sort the collection of As is greater than that of the Bs. But, thereupon, there at once arises the question, why may not two collections each be greater than the other? Now if that be possible, the idea of magnitude breaks down. There are logico-mathematicians who think it is possible.

But there are others, Cantor among them, who think not. To me the notion that every one-to-one relation between As and Bs should leave over some A·s unrelated to any Bs although there are Bs to which no As are related, and that there should be no relation whatever in which these unoccupied As could stand to those unoccupied Bs is contrary to the nature of relation and of possibility.

If by the possible you mean no more than that which you do not know to be false, then everything in mathematics not already demonstrated to be false is possible. No doubt, that logical situation is the basis of the conception of possibility. But so definin,g the possible a relation of the kind in question is possible until you have demonstrated that the collections of [the] As and of the Bs have definite characters which conflict with the supposition that there is such a relation. But I think it would be more convenient to say not that everything in mathematics about which you happen to be ignorant is possible but that only that is possible of whose falsity no demonstration ever will be given. The question then would be whether anything can render it demonstrable that the As cannot be put into a one-to-one relation to Bs except by showing that there are no Bs for them to be in one to one relation to. Now it is plain there cannot be such a demonstration.

It cannot be said that this definition of possibility is satisfactory.

Not to trouble you with logical subtleties where I can avoid it, let us say that an assertion is general if no amount of actual fact could certainly fulfill the truth of it. It says you never will find this falsified. The future never will have been exhausted. A general assertion, leaves it to the hearer to take any instance he can. To say “all men are mortal” is as much to say, you can take any man you please, and experience will prove he is a liar [sic].

Of an opposite kind are indefinite assertions, where the speaker does not fully commit himself as to what is the instance he is speaking of. As the general is that which no amount of fact can constitute true, so the indefinite is that which no amount of fact can constitute false; for its asserter only says the future will produce a case of such and such a kind.

These two definitions will be found helpful in discussing the question whether or not two collections can be each greater than the other. But first we must answer the question, What is meant by a collection? I answer, It is a whole of ultimate parts which are discrete objects. What, then, is meant by discrete objects? I answer, objects which, whether it be in human power to distinguish them, are supposed to be in themselves of such a nature as to be susceptible of being so described that every one is distinguished from every other. In other words by discrete objects are meant individuals of a system of definite individuals — Definite each in its own nature although we may not be able to define them singly.

That being the case, I assert that given any definite collection whatsoever, there is some general character which belongs to all its members and belongs to nothing else, a character common and peculiar to the members of that collection. For if it were not so, the collection would not be a definite collection. If it were not so, you could instance such a collection. “Very well” you would say, “look there!” Look where, I should naturally ask; and you would have either to describe the collection unmistakably when your description would involve a common and peculiar character of its members, or you would have to do something bringing that collection and no other to my attention when you would create such a character. If you object that that character would not have existed before you had created it, I should reply that all general characters refer to what will take place in the future. Now relations are characters of sets of objects; and therefore the proposition just enunciated includes the proposition that there is [a] dyadic relation common and peculiar to all the pairs of objects of a collection.

Lowell Lecture 6