Category: Meaning and Modeling

Aspects of your internal model make a difference to your practice by functioning as precepts. (This is a version of Peirce’s pragmaticism.) This of course includes your practice of inquiry and reasoning, where precepts guide observation or perception. Peirce explains that the subject of a proposition, which acts like an index in directing attention to some singular object, ‘may be a precept by following which a singular could be found’ (EP2:168; follow this link for context).

A scientific model is one from which testable predictions can be deduced in the form of conditional propositions. Strictly speaking, truth belongs to propositions, not to models. We can test our predictions by comparing them with the results of our experiments, but we cannot compare a sign with its object, a word with its meaning, or a message with its source.

We can’t even compare one model with another, unless some ground of comparison exists which amounts to a more comprehensive model.

It is generally admitted that science is fallible, but often the progress of inquiry is expressed in terms of ‘approximation’ to the truth – as if we could step back and measure how close we were to some absolute reality. This in itself is a model of the process of inquiry, incorporating a more or less mathematical diagram: we imagine ourselves (i.e. our consensus) approaching the truth, in the way that geometrical curve approaches an asymptote (i.e. without ever quite arriving at it).

When a theory works better than previous theories, and has been applied successfully in many situations for a long time, we begin to think of it as a ‘law of nature.’ We have no way of knowing whether some other (as yet unimagined) theory would serve equally well, but if the theory in question seems coherent with other established theories, it gradually becomes integrated into our general model of the world.

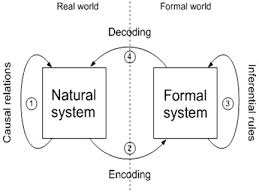
The gnoxic meaning-cycle diagram, and Rosen’s diagram of the modeling relation, are diagrams of semiosis, Thirdness and thought in the Peircean sense. As Peirce said (Chapter 10), ‘Thirdness is found wherever one thing brings about a Secondness between two things.’ This follows from Peirce’s highly abstract definitions of the elements of the phaneron:

Firstness is that which is such as it is positively and regardless of anything else.

Secondness is that which is as it is in a second something’s being as it is, regardless of any third.

Thirdness is that whose being consists in its bringing about a secondness.

EP2:267

The ‘something’ or subject in the mode of being called Secondness is as it is in being Second to something else, an Other (but not a significant Other, as significance would be a third). In our gnoxic diagram, W exists as such by virtue of its Secondness to the system or subject to whom it is external; and this Secondness or reactivity is mutual. On the other side of the diagram, M is a ‘model’ by virtue of its dyadic relation to W, a secondness ‘brought about’ by semiosis, the process represented by the arrows in the diagram. But within that process, M can be regarded as a sign which, in its Thirdness or mediation between the subject and its world, brings them into actual relation with each other by directing the actions and attention of the subject (upper arrow), while also being an interpretant of a perceptual sign-complex.

The lower arrow in our diagram represents the action of a ‘natural sign’ in bringing about a subject’s experience of that other subject which is the object of that sign; the Secondness is the experiential relation or ‘reaction’ between those two subjects. The upper arrow represents the action of an intentionally ‘uttered sign’ (Peirce, CP 8.348, EP2:484), or an act of communication directed from one subject (the utterer) to another (the interpreter), which brings about in the latter subject the embodiment of a Form which was already embodied in the former. This ‘embodiment’ or alteration of bodymind is a Secondness brought about by the sign.

Another way of reading the diagram would see the lower arrow as representing the compulsiveness of W’s effect on M in perception, while the upper arrow represents the effect of actual practice on W. Each of these is a Secondness brought about by the function of the guidance system (the modeling relation, the meaning cycle) which governs both ception and practice. In ception, ‘the third is thought in its role as governing Secondness. It brings the information into the mind, or determines the idea and gives it body. It is informing thought, or cognition’ (CP 1.537). In practice, the Thirdness is that of ‘a habit, which determines the suchness of that which may come into existence, when it does come into existence’ (Peirce, EP2:269). This is also the way laws of nature govern what happens in nature – which brings us round to W again.

The Thirdness of a sign determines what kind of relation, or ‘correspondence,’ two things will have:

I define a sign as something, A, which brings something, B, its interpretant, into the same sort of correspondence with something, C, its object, as that in which itself stands to C.

— Peirce, MS L75.235 (1902)

Here B and C are the two things brought into relation by the mediating function of A, the sign. But this ‘bringing into correspondence’ is also a continuous process in which A, B and C are all signs. Within this process, the ‘immediate object which any sign seeks to represent is itself a sign,’ and so is its interpretant; we can analyze the process ad infinitum, giving us ‘two infinite series, the one back toward the object, the other forward toward the interpretant’ (see above). At the limits of these infinite series stand the dynamic object and the final interpretant. At any “point” (or rather any moment) along the way of semiosis, the object and interpretant are immediate.

The term ‘scientific model’ usually refers to conceptual or computer models, not tangible physical structures. One famous episode in science which did involve tangible models was the 1953 discovery by Crick and Watson of the double-helix structure of DNA. Their rod-and-ball constructions, ‘which looked like Tinker Toys gone crazy’ (Depew and Weber 1995, 346), enabled them to ‘scoop’ Rosalyn Franklin, from whom they extracted crucial information leading to the discovery. ‘Unlike Franklin, who would otherwise have been in a good position to deduce DNA’s structure, they were not patient enough to be empiricists’ (Depew and Weber 1995, 345). In other words they used the abductive logic of guess-and-modify rather than the inductive logic of starting with the evidence and methodically building the theory from that ground up; and abductive logic is often facilitated by working with models which are visible (if not tangible). But like all models, the Watson-Crick model greatly simplified the reality, which is far more dynamic, fluctuating at several different time scales (Pagels 1988, 107).

The same is true of anyone’s internal model of the world one has to navigate. When we said in Chapter 3 that ‘map’ is a misleading word because the world in which an animal moves is multidimensional, even that was a gross understatement; see Llinás (2001, Chapter 2) on the ‘dimensionality of the problem of motor control’ (26). In the same chapter, Llinás explains guidance systems in a way quite similar to Varela’s ‘enactive’ model (as outlined in the Chapter 9). ‘The brain’s control of organized movement gave birth to the generation and nature of the mind’ (50); ‘that which we call thinking is the evolutionary internalization of movement’ (35). In the Llinás model, the ‘8-12 Hz rhythmicity of physiological tremor’ (31) acts as the ‘clock’ which enables synchronization of movement. All movement is a modulation of this ever-present ‘tremor,’ which is its material cause; when the organism reacts to external events, sensory input is the efficient cause. But an organism can also initiate movement proactively.

As emphasized in Chapter 10, it should be clear in our reading of the meaning-cycle diagram ‘that the flow from M to W is simultaneous with the flow from W to M. There is only one flow, not two taking turns.’ Within the brain, the functional unity of action and perception is embodied in ‘mirror neurons’ and in the

class of neurons in the frontal lobes called canonical neurons.… Like mirror neurons, each canonical neuron fires during the performance of a specific action such as reaching for a vertical twig or an apple. But the same neuron will also fire at the mere sight of a twig or an apple. In other words, it is as though the abstract property of graspability were being encoded as an intrinsic aspect of the object’s visual shape. The distinction between perception and action exists in our ordinary language, but it is one that the brain evidently doesn’t always respect.

— Ramachandran 2011 (Kindle Locations 938-943)

The ‘theory theory’ of an ‘infantile scientific impulse’ and Rosen’s concept of anticipatory systems were both anticipated by Peirce. In a 1901 article, he used ‘a little diagrammatic psychology’ to sketch the origins of the scientific quest for truth:

No man can recall the time when he had not yet begun a theory of the universe, when any particular course of things was so little expected that nothing could surprise him, even though it startled him. The first surprise would naturally be the first thing that would offer sufficient handle for memory to draw it forth from the general background. It was something new. Of course, nothing can appear as definitely new without being contrasted with a background of the old. At this, the infantile scientific impulse,— what becomes developed later into various kinds of intelligence, but we will call it the scientific impulse because it is science that we are now endeavoring to get a general notion of,— this infantile scientific impulse must strive to reconcile the new to the old. The first new feature of this first surprise is, for example, that it is a surprise; and the only way of accounting for that is that there had been before an expectation. Thus it is that all knowledge begins by the discovery that there has been an erroneous expectation of which we had before hardly been conscious. Each branch of science begins with a new phenomenon which violates a sort of negative subconscious expectation, like the frog’s legs of Signore Galvani.

— EP2:87-8

Later on the same page, Peirce integrated emotion into this cognitive picture by observing that ‘the emotion of surprise’ which triggers inquiry ‘is merely the instinctive indication of the logical situation. It is evolution (φύσις) that has provided us with the emotion. The situation is what we have to study.’

Kant, in his Critique of Judgment, distinguished between ‘machines, moved by a mere driving force, bewegende Kraft’ and ‘organisms moved internally by a bildende Kraft, a capacity, a formative force’ (Eco 1997, 93). Bildende could be translated without much distortion as ‘modeling’ or ‘anticipatory’ in Rosen’s sense.

The crucial difference between an organism and a machine, according to Rosen, is that any ‘machine’ has a largest model that can completely describe it, while a living system does not. This is a mathematical expression of the idea that an organism is constantly reinventing itself, and indeed is doing this by modifying its own internal models. Any external model would therefore have to leave room for that creativity by representing its own incompleteness. This could be taken as the point of Terrence Deacon’s Incomplete Nature (see Chapter 10 and 11), and perhaps of Peirce’s remark that an abstract statement could claim to be true only ‘by virtue of the confession of its inaccuracy and one-sidedness,’ this ‘confession’ being ‘an essential ingredient of truth.’

Building or learning a new model (such as Rosen’s model of modeling or Gendlin’s process model), you first throw a line across (like an orbweaving spider) from your current standpoint to the new one, and then carry terms across this bridge from the old model to the new, one or a few at a time. (Writing consolidates this process, as anyone who has tried it can testify.) This changes the meanings of terms you were using before but are now using for the new model, which becomes the implicit context of your habitual usage of those terms you carried across to it.

What we call ‘knowledge’ is just that property of Rosen’s ‘anticipatory systems’ which enables them to anticipate successfully (to some degree). Karl Popper points in this direction when he says that ‘knowledge has often the character of expectations’ and that ‘most kinds of knowledge, whether of men or animals, are hypothetical or conjectural’ (Popper 1990, 32).

One rendering of Rosen’s original (1991) diagram (described in Chapter 10) looks like this:
It was Rosen who wrote the book on ‘anticipatory systems,’ but it has been widely recognized that anticipation is the key to guidance. Polanyi, for instance, remarked that our ‘whole set of faculties—our conceptions and skills, our perceptual framework and our drives—’ amount to ‘one comprehensive power of anticipation’ (Polanyi 1962, 103). Our meaning-cycle diagram is a way of picturing the form of that power, and the following passage from Polanyi could serve as a caption to it:

Why do we entrust the life and guidance of our thoughts to our conceptions? Because we believe that their manifest rationality is due to their being in contact with domains of reality, of which they have grasped one aspect. This is why the Pygmalion at work in us when we shape a conception is ever prepared to seek guidance from his own creation; and yet, in reliance on his contact with reality, is ready to re-shape his creation, even while he accepts its guidance. We grant authority over ourselves to the conceptions which we have accepted, because we acknowledge them as intimations—derived from the contact we make through them with reality—of an indefinite sequence of novel future occasions, which we may hope to master by developing these conceptions further, relying on our own judgment in its continued contact with reality. The paradox of self-set standards is re-cast here into that of our subjective self-confidence in claiming to recognize an objective reality.

— Polanyi (1962, 104)

According to Howard Pattee (personal communication), Rosen first developed this diagram as a graphical representation of Heinrich Hertz’s description of the modeling process. (Pattee was working with Rosen at the Center for Theoretical Biology at Buffalo in the early 1970s, ‘when he was developing the ideas in Anticipatory Systems where his modeling diagram first appears.’) Hertz described the modeling process as follows:

We form for ourselves images or symbols of external objects; and the form which we give them is such that the logically necessary (denknotwendigen) consequents of the images in thought are always the images of the necessary natural (naturnotwendigen) consequents of the thing pictured.

For our purpose it is not necessary that they [images] should be in conformity with the things in any other respect whatever. As a matter of fact, we do not know, nor have we any means of knowing, whether our conception of things are in conformity with them in any other than this one fundamental respect.

— Hertz, The Principles of Mechanics, 1-2 (New York: Dover, 1984; original German edition, Prinzipien Mechanik, 1894)

This confirms Einstein’s point that the ‘natural system’ we are modeling is unknowable, in the sense that its inner workings are not directly observable. As modelers, we make an ‘epistemic cut’ (Pattee) between image and reality. The correspondence which defines the modeling relation as such is between the observed “behavior” of the “real” system (arrow #1, ‘causality’) and the ‘logically necessary consequents of the images in thought’ (arrow #3, ‘inference’).

This brings out a crucial point which is not clearly represented in the diagram: that any relevant act of observation takes time. In fact, every ‘observation’ or ‘measurement’ in science must consist of (at least) two measurements: one of the initial conditions, and another (some time later) after the system has ‘behaved’ in the situation we have chosen to focus on. What we call ‘the measurement’ is really the difference between these two measurements (even if it is zero because the system has not changed within the time frame). This is what Bateson calls ‘news of a difference’ (and Rosen calls ‘encoding’ – arrow #2). A theoretical model ‘works’ when that difference corresponds to some specific difference between states of the theoretical image, some aspect of the model’s dynamics.

Pattee adds that the diagram ‘also does not make clear that in a biological system the consequent of the model can be used to control its own state. The genetic description is a kind of model that exercises this kind of control of its own synthesis. This dependence of life on models or descriptions is what motivates the field of biosemiotics.’

To the contemplative, action furnishes material for reflection. To the activist, reflection gives guidance for action. Meaning arises from the interplay between the two.

The trick of reason is to get the imagination to seize the actual world—if only from time to time.

— Annie Dillard (2009, 143)

The English word theory derives from a Greek root meaning either contemplation or being a spectator or onlooker, as in the theater. In purely theoretical science, one takes on the role of spectator rather than actor, so that he is not “trying to prove” his own idea. Continue reading Theory